题目内容
6.椭圆x2+$\frac{{y}^{2}}{m}$=1的焦点在x轴上,长轴长是短轴长的两倍,则m的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
分析 由题意可得a2=1,b2=m,求出a,b的值,结合长轴长是短轴长的两倍列式求得m值.
解答 解:∵椭圆${x^2}+\frac{y^2}{m}=1$的焦点在x轴上,
∴a2=1,b2=m,则a=1,b=$\sqrt{m}$,
又长轴长是短轴长的两倍,
∴2=$4\sqrt{m}$,即m=$\frac{1}{4}$.
故选:A.
点评 本题考查椭圆的简单性质,是基础的计算题.

练习册系列答案
相关题目
16.已知函数f(x)=ln(1+x2),则满足不等式f(2x-1)<f(3)的x的取值范围是( )
| A. | (-∞,2) | B. | (-2,2) | C. | (-1,2) | D. | (2,+∞) |
15.如图所示,四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得到AB∥面MNP的图形的序号是( )
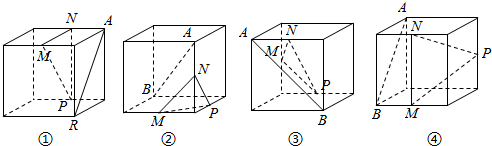

| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |
