题目内容
(本小题满分14分)已知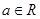 且
且 ,设函数
,设函数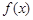 = ax2 +x-3alnx.
= ax2 +x-3alnx.
(I)求函数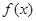 的单调区间;
的单调区间;
(II)当a=-1时,证明: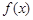 ≤2x-2.
≤2x-2.
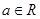 且
且 ,设函数
,设函数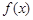 = ax2 +x-3alnx.
= ax2 +x-3alnx.(I)求函数
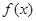 的单调区间;
的单调区间;(II)当a=-1时,证明:
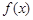 ≤2x-2.
≤2x-2.(I)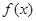 的单调递增区间为(0,
的单调递增区间为(0,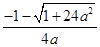 )、递减区间为(
)、递减区间为(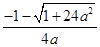 ,
,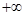 ); (II)见解析。
); (II)见解析。
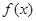 的单调递增区间为(0,
的单调递增区间为(0,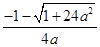 )、递减区间为(
)、递减区间为(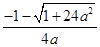 ,
,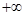 ); (II)见解析。
); (II)见解析。试题分析:(I)先求出
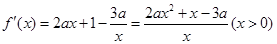 ,然后再根据导数大于(小于)零,分别求出其单调增(减)区间.
,然后再根据导数大于(小于)零,分别求出其单调增(减)区间.(II)当a=-1时,
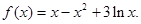 ,然后构造函数
,然后构造函数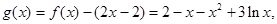 再利用导数求g(x)的最大值,证明其最大值不大于零即可.
再利用导数求g(x)的最大值,证明其最大值不大于零即可.(I)
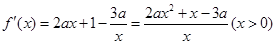 …………………………1分
…………………………1分令
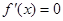 解得
解得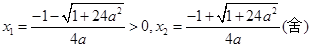 …………………3分
…………………3分列表如下:
| x | (0,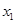 ) ) | | (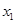 , ,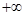 ) ) |
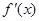 | + | | - |
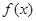 |  | |  |
故
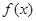 的单调递增区间为(0,
的单调递增区间为(0,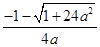 )、递减区间为(
)、递减区间为(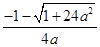 ,
,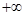 )…………………7分
)…………………7分(II)
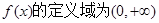 ,a=-1时,
,a=-1时,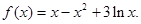
设
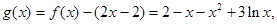 ………………………………9分
………………………………9分则
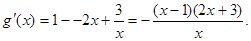 ……………………10分
……………………10分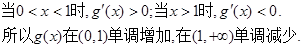 ……………………12分
……………………12分而
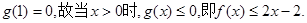 ……………………14分
……………………14分点评:利用导数求单调区间时:如果含有参数,要注意分类讨论,并且要注意函数的定义域.
证明不等式的问题可以通过构造函数,通过导数研究函数的最值证明不等式是常用的策略之一.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
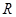 的单调函数
的单调函数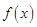 是奇函数,当
是奇函数,当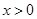 时,
时,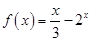 .
.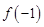 的值;
的值;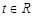 ,不等式
,不等式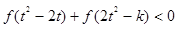 恒成立,求实数
恒成立,求实数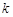 的取值范围.
的取值范围.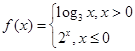 ,则
,则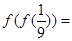 ( )
( )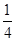
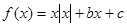 ,给出以下四个命题:①当c=0时,有
,给出以下四个命题:①当c=0时,有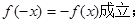 ②当b=0,c>0时,方程
②当b=0,c>0时,方程 ③函数
③函数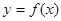 的图象关于点(0,c)对称 ④当x>0时;函数
的图象关于点(0,c)对称 ④当x>0时;函数 。其中正确的命题的序号是_________。
。其中正确的命题的序号是_________。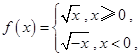 且
且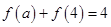 ,那么
,那么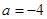 ;
;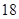 ,
,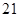 ,
,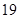 ,
,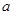 ,
,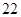 的平均数是
的平均数是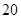 ,那么这组数据的方差是
,那么这组数据的方差是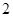 ;
; 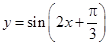 的图象,只要将
的图象,只要将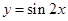 的图象向左平移
的图象向左平移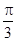 单位;
单位;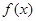 在
在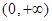 为增函数,且
为增函数,且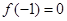 ,则不等式
,则不等式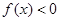 的解集为
的解集为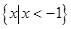 .
. 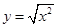 与
与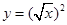
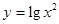 与
与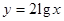
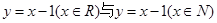
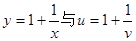
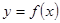 的图像的有几个( )
的图像的有几个( )
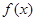 的定义域为
的定义域为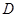 ,若存在闭区间
,若存在闭区间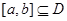 ,使得函数
,使得函数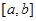 内是单调函数;②
内是单调函数;②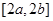 ,则称区间
,则称区间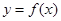 的“倍值区间”.下列函数中存在“倍值区间”的有
的“倍值区间”.下列函数中存在“倍值区间”的有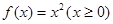 ; ②
; ②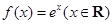 ;
;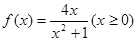 ; ④
; ④