题目内容
已知命题P:实数m满足方程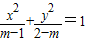 表示焦点在y轴上的椭圆,命题q:实数m满足m2-7am+12a2<0(a>0),且p是q的必要不充分条件,求a的取值范围.
表示焦点在y轴上的椭圆,命题q:实数m满足m2-7am+12a2<0(a>0),且p是q的必要不充分条件,求a的取值范围.
【答案】分析:已知命题P,根据椭圆的性质,可以求出m的范围,命题q:实数m满足m2-7am+12a2<0(a>0),利用因式分解法求出m的范围,再根据p是q的必要不充分条件,即q⇒p,从而求出a的取值范围;
解答:解:命题P:实数m满足方程 表示焦点在y轴上的椭圆,
表示焦点在y轴上的椭圆,
p: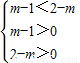
解得:1<m< ;
;
q:∵实数m满足m2-7am+12a2<0(a>0),∴(m-3a)(m-4a)<0,
∴3a<m<4a(a>0)…(4分)
依题意,p是q的必要不充分条件,有q⇒p且p≠>q…(6分)
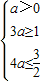
解得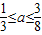 …(12分)
…(12分)
点评:此题主要考查充分必要条件的定义,以及椭圆的性质,利用十字相乘法求m2-7am+12a2<0的解集,是解决此题的关键,是一道中档题;
解答:解:命题P:实数m满足方程
 表示焦点在y轴上的椭圆,
表示焦点在y轴上的椭圆,p:
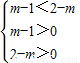
解得:1<m<
 ;
;q:∵实数m满足m2-7am+12a2<0(a>0),∴(m-3a)(m-4a)<0,
∴3a<m<4a(a>0)…(4分)
依题意,p是q的必要不充分条件,有q⇒p且p≠>q…(6分)
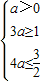
解得
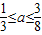 …(12分)
…(12分)点评:此题主要考查充分必要条件的定义,以及椭圆的性质,利用十字相乘法求m2-7am+12a2<0的解集,是解决此题的关键,是一道中档题;

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目