题目内容
已知命题p：实数m满足m-1≤0，命题q：函数y=（9-4m）x是增函数．若p∨q为真命题，p∧q为假命题，则实数m的取值范围为
（1，2）
（1，2）
．分析：由题设知命题p：m≤1，命题q：m＜2，由p∨q为真命题，p∧q为假命题，知p真q假，或p假q真．由此能求出m的取值．
解答：解：∵命题p：实数m满足m-1≤0，命题q：函数y=（9-4m）x是增函数，
∴命题p：m≤1，命题q：9-4m＞1，m＜2，
∵p∨q为真命题，p∧q为假命题，
∴p真q假，或p假q真．
当p真q假时，
，无解；
当p假q真时，
，故1＜m＜2．
故答案为：（1，2）．
∴命题p：m≤1，命题q：9-4m＞1，m＜2，
∵p∨q为真命题，p∧q为假命题，
∴p真q假，或p假q真．
当p真q假时，
|
当p假q真时，
|
故答案为：（1，2）．
点评：本题考查复合命题的真假判断，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
，命题q：实数x满足x2-2x+（1-m2）≤0（m＞0），若¬p是¬q的必要不充分条件，求实数m的取值范围．
，命题q：实数x满足x2-2x+（1-m2）≤0（m＞0），若¬p是¬q的必要不充分条件，求实数m的取值范围．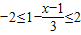
，命题q：实数x满足x2-2x+（1-m2）≤0（m＞0），若¬p是¬q的必要不充分条件，求实数m的取值范围．