题目内容
已知命题p：实数m满足m2-7am+12a2＜0（a＞0），命题q：实数m满足方程
+
=1表示焦点在y轴上的椭圆，且非q是非p的充分不必要条件，求a的取值范围．
| x2 |
| m-1 |
| y2 |
| 2-m |
分析：根据命题p、q分别求出m的范围，再根据非q是非p的充分不必要条件列出关于m的不等式组，解不等式组即可
解答：解：由m2-7am+12a2＜0（a＞0），则3a＜m＜4a
即命题p：3a＜m＜4a
由
+
=1表示焦点在y轴上椭圆可得：2-m＞m-1＞0，∴1＜m＜
即命题q：1＜m＜
由非q为非p充分不必要条件，则p是q的充分不必要条件
从而有：
∴
≤a≤
即命题p：3a＜m＜4a
由
| x2 |
| m-1 |
| y2 |
| 2-m |
| 3 |
| 2 |
即命题q：1＜m＜
| 3 |
| 2 |
由非q为非p充分不必要条件，则p是q的充分不必要条件
从而有：
|
∴
| 1 |
| 3 |
| 3 |
| 8 |
点评：本题考查充分条件、必要条件，一元二次不等式的解法，椭圆的定义等相关知识，要求对基础知识有比较好的把握．属简单题
练习册系列答案
发散思维新课堂系列答案
相关题目
，命题q：实数x满足x2-2x+（1-m2）≤0（m＞0），若¬p是¬q的必要不充分条件，求实数m的取值范围．
，命题q：实数x满足x2-2x+（1-m2）≤0（m＞0），若¬p是¬q的必要不充分条件，求实数m的取值范围．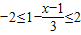
，命题q：实数x满足x2-2x+（1-m2）≤0（m＞0），若¬p是¬q的必要不充分条件，求实数m的取值范围．