题目内容
若数列{an}的通项公式an=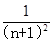 ,记f(n)=2(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________
,记f(n)=2(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________
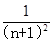 ,记f(n)=2(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________
,记f(n)=2(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________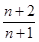
解:f(1)=2(1-a1)=3/2=(1+2)/(1+1),
f(2)=2(1-1/4)(1-1/9)=4/3=(2+2)/(2+1),
f(3)=2(1-a1)(1-a2)(1-a3)
=2(1-1/4)(1-1/9)(1-1/16)=5/4=(3+2)/(3+1),
可猜测f(n)=(n+2)/(n+1).
f(2)=2(1-1/4)(1-1/9)=4/3=(2+2)/(2+1),
f(3)=2(1-a1)(1-a2)(1-a3)
=2(1-1/4)(1-1/9)(1-1/16)=5/4=(3+2)/(3+1),
可猜测f(n)=(n+2)/(n+1).

练习册系列答案
相关题目
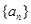 的首项
的首项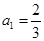 ,
,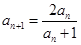 ,
,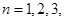 ….
….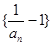 是等比数列; (Ⅱ)求数列
是等比数列; (Ⅱ)求数列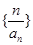 的前
的前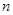 项和
项和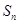
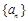 的前n项和为
的前n项和为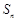 ,
,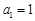 ,且
,且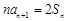 (
(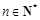 ),数列
),数列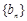 满足
满足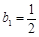 ,
,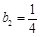 ,对任意
,对任意 .
.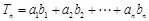 ,若对任意的
,若对任意的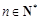 ,不等式
,不等式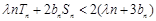 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.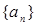 的首项
的首项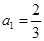 ,
,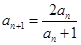 ,
,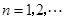 .
.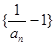 是等比数列;
是等比数列;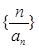 的前
的前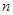 项和
项和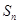 .
.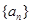 的前n项和为
的前n项和为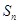 ,且
,且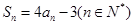 。
。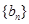 满足
满足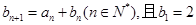 ,求数列
,求数列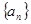 中,
中,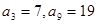 ,则
,则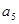 为()
为()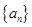 的前
的前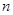 项和为
项和为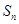 ,若
,若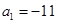 ,
,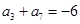 ,则当
,则当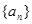 中,
中,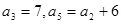 ,则
,则 .
.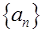 中,
中, 则
则 的值等于
的值等于