题目内容
已知数列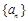 的前n项和为
的前n项和为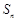 ,
,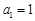 ,且
,且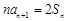 (
(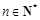 ),数列
),数列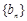 满足
满足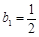 ,
,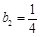 ,对任意
,对任意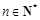 ,都有
,都有 .
.
(Ⅰ)求数列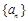 、
、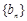 的通项公式;
的通项公式;
(Ⅱ)令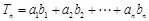 ,若对任意的
,若对任意的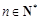 ,不等式
,不等式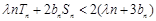 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.
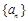 的前n项和为
的前n项和为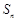 ,
,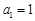 ,且
,且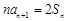 (
(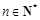 ),数列
),数列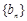 满足
满足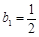 ,
,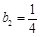 ,对任意
,对任意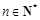 ,都有
,都有 .
.(Ⅰ)求数列
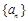 、
、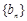 的通项公式;
的通项公式;(Ⅱ)令
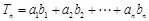 ,若对任意的
,若对任意的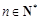 ,不等式
,不等式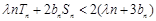 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.(Ⅰ)∵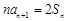 ,∴
,∴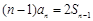 (
(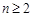 ),两式相减得,
),两式相减得,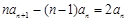 ,
,
∴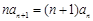 ,即
,即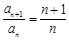 ,∴
,∴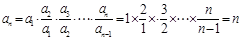 (
(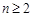 ),
),
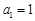 满足上式,故数列
满足上式,故数列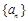 的通项公式
的通项公式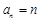 (
(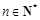 ).··········· 4分
).··········· 4分
在数列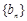 中,由
中,由 ,知数列
,知数列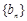 是等比数列,首项、公比均为
是等比数列,首项、公比均为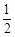 ,
,
∴数列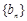 的通项公式.(若列出
的通项公式.(若列出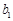 、
、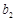 、
、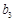 直接得
直接得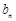 而没有证明扣1分)···· 6分
而没有证明扣1分)···· 6分
(Ⅱ)∴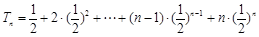 ①
①
∴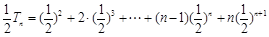 ②
②
由①-②,得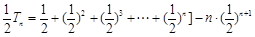
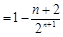 ,
,
∴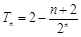 ,·························· 8分
,·························· 8分
不等式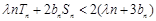 即为
即为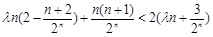 ,
,
即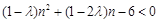 (
(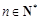 )恒成立.··············· 9分
)恒成立.··············· 9分
方法一、设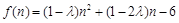 (
(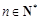 ),
),
当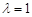 时,
时,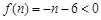 恒成立,则
恒成立,则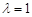 满足条件;
满足条件;
当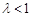 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;
当 时, 由于
时, 由于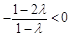 ,则
,则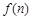 在
在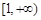 上单调递减,
上单调递减,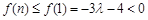 恒成立,则
恒成立,则 满足条件.
满足条件.
综上所述,实数λ的取值范围是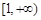 .··············· 12分
.··············· 12分
方法二、也即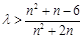 (
(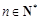 )恒成立,·············· 9分
)恒成立,·············· 9分
令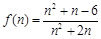 .则
.则 ,·· 10分
,·· 10分
由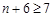 ,
,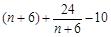 单调递增且大于0,∴
单调递增且大于0,∴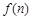 单调递增,当
单调递增,当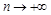 时,
时,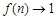 ,且
,且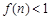 ,故
,故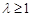 ,∴实数λ的取值范围是
,∴实数λ的取值范围是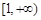 .
.
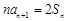 ,∴
,∴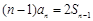 (
(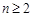 ),两式相减得,
),两式相减得,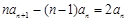 ,
,∴
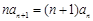 ,即
,即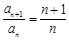 ,∴
,∴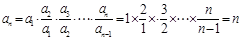 (
(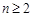 ),
),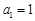 满足上式,故数列
满足上式,故数列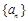 的通项公式
的通项公式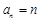 (
(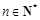 ).··········· 4分
).··········· 4分在数列
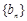 中,由
中,由 ,知数列
,知数列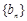 是等比数列,首项、公比均为
是等比数列,首项、公比均为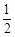 ,
,∴数列
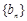 的通项公式.(若列出
的通项公式.(若列出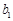 、
、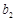 、
、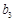 直接得
直接得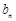 而没有证明扣1分)···· 6分
而没有证明扣1分)···· 6分(Ⅱ)∴
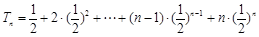 ①
①∴
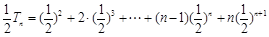 ②
②由①-②,得
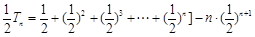
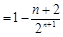 ,
,∴
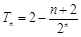 ,·························· 8分
,·························· 8分不等式
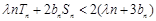 即为
即为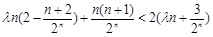 ,
,即
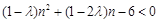 (
(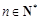 )恒成立.··············· 9分
)恒成立.··············· 9分方法一、设
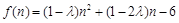 (
(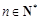 ),
),当
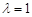 时,
时,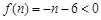 恒成立,则
恒成立,则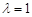 满足条件;
满足条件;当
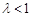 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;当
 时, 由于
时, 由于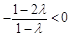 ,则
,则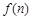 在
在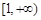 上单调递减,
上单调递减,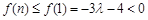 恒成立,则
恒成立,则 满足条件.
满足条件.综上所述,实数λ的取值范围是
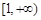 .··············· 12分
.··············· 12分方法二、也即
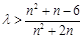 (
(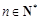 )恒成立,·············· 9分
)恒成立,·············· 9分令
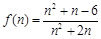 .则
.则 ,·· 10分
,·· 10分由
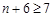 ,
,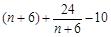 单调递增且大于0,∴
单调递增且大于0,∴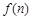 单调递增,当
单调递增,当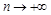 时,
时,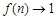 ,且
,且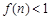 ,故
,故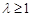 ,∴实数λ的取值范围是
,∴实数λ的取值范围是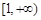 .
.略

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
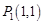 ,
,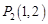 ,
,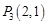 ,
,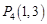 ,
,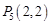 ,
,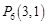 ,
,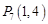 ,
,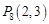 ,
,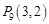 ,
,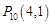 ,
,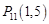 ,
,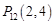 ,……,则
,……,则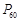 的坐标为( )
的坐标为( )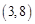
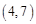
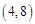
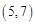
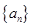 的前
的前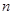 项和为
项和为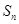 ,若
,若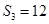 ,且
,且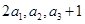 成等比数列.
成等比数列.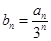 ,记数列
,记数列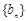 的前
的前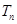 ,求
,求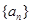 的前
的前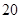 项的和
项的和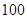 ,那么
,那么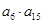 最大值是
最大值是 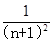 ,记f(n)=2(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________
,记f(n)=2(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)=________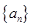 满足:
满足: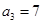 ,
,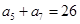 ,
,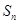 .
.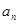 及
及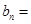
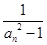 (n
(n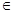 N*),求数列
N*),求数列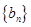 的前n项和
的前n项和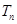 .
. 的项数是( ).
的项数是( ).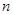
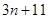
 的前n项和为
的前n项和为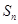 ,若
,若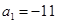 ,
,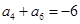 ,则当
,则当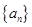 满足
满足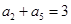 ,则
,则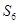 的值为( )
的值为( )