题目内容
6.已知函数f(x)=$\frac{kx+b}{{e}^{x}}$,曲线y=f(x)在点(0,f(0))处的切线方程为x-y=0.(I)求k,b的值;
(Ⅱ)求函数f(x)的零点个数.
分析 (I)求导数,利用曲线y=f(x)在点(0,f(0))处的切线方程为x-y=0,建立方程,即可求k,b的值;
(Ⅱ)求导数,求得函数在(-∞,1)上单调递增,在(1,+∞)上单调递减,即可求函数f(x)的零点个数.
解答 解:(I)∵f(x)=$\frac{kx+b}{{e}^{x}}$,
∴f′(x)=$\frac{k-kx-b}{{e}^{x}}$
∵曲线y=f(x)在点(0,f(0))处的切线方程为x-y=0,
∴f′(0)=$\frac{k-b}{e}$=1,f(0)=$\frac{b}{{e}^{0}}$=0,
∴k=e,b=0;
(Ⅱ)f(x)=$\frac{x}{{e}^{x-1}}$,f′(x)=$\frac{1-x}{{e}^{x-1}}$,
∴函数在(-∞,1)上单调递增,在(1,+∞)上单调递减,
∵f(1)=1>0
∴函数f(x)的零点个数是2个.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性,确定函数的解析式是关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
15.函数y=x-$\frac{1}{x}$在[1,2]上的最大值为( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
16.有5种不同的作物,从中选出三种分别种在三种不同的土质的试验小区内,其中甲、乙两种作物不种在1号小区内的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | 1 |
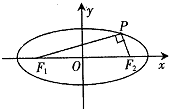 如图,P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=90°,则|PF1|•|PF2|等于( )
如图,P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=90°,则|PF1|•|PF2|等于( ) 某连锁火锅城开业之际,为吸引更多的消费者,开展抽奖活动,前20位顾客可参加如下活动:摇动如图所示的游戏转盘(上面扇形的圆心角都相等),顾客可以免费获得按照指针所指区域的数字10倍金额的店内菜品或饮品,最高120元,每人只能参加一次这个活动.记事件A:获得不多于30元菜品或饮品.
某连锁火锅城开业之际,为吸引更多的消费者,开展抽奖活动,前20位顾客可参加如下活动:摇动如图所示的游戏转盘(上面扇形的圆心角都相等),顾客可以免费获得按照指针所指区域的数字10倍金额的店内菜品或饮品,最高120元,每人只能参加一次这个活动.记事件A:获得不多于30元菜品或饮品.