题目内容

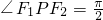设F₁、F₂是椭圆 $数学公式$ 的两个焦点，点P在椭圆上，且满足 $数学公式$ ，则△F₁PF₂的面积等于________．

1
分析：利用椭圆的定义可得|PF₁|+|PF₂|=4，又|F₁F₂|=2 $\text{[math]}$ ，∠F₁PF₂= $\text{[math]}$ ，利用余弦定理可求得|PF₁|•|PF₂|，从而可求得△F₁PF₂的面积．
解答：∵P是椭圆 $\text{[math]}$ 上的一点，F₁、F₂是椭圆的两个焦点，∠F₁PF₂= $\text{[math]}$ ，
∴|PF₁|+|PF₂|=4，|F₁F₂|=2 $\text{[math]}$ ，
在△F₁PF₂中，由勾股定理得：
|F₁F₂|²=|PF₁|²+|PF₂|²=（|PF₁|+|PF₂|）²-2|PF₁|•|PF₂|
=16-2|PF₁|•|PF₂|=16-2|PF₁|•|PF₂|=12，
∴|PF₁|•|PF₂|=2，
∴S△F₁PF₂= $\text{[math]}$ |PF₁|•|PF₂|=1
故答案为：1
点评：本题考查椭圆的简单性质与标准方程，考查勾股定理与三角形的面积，属于中档题．

练习册系列答案

高分拔尖提优训练系列答案

聚焦课堂高效学习直通车系列答案

小题巧练系列答案

教材补充练习系列答案

长江作业本同步练习册系列答案

创优课时训练系列答案

简易通系列答案

课时精练与精测系列答案

全易通系列答案

小学创新一点通系列答案

相关题目

设F₁，F₂是椭圆的两个焦点，F₁F₂=8，P是椭圆上的点，PF₁+PF₂=10，且PF₁⊥PF₂，则点P的个数是

设F₁、F₂是椭圆的两个焦点，P是椭圆上一点，且P到两个焦点的距离之差为2，则△PF₁F₂是（　　）

A.钝角三角形 B.锐角三角形

C.斜三角形 D.直角三角形

（本题20分，第1小题满分4分，第2小题满分6分，第3小题6分，第4小题4分）

我们知道，判断直线与圆的位置关系可以用圆心到直线的距离进行判别，那么直线与椭圆的位置关系有类似的判别方法吗？请同学们进行研究并完成下面问题。

（1）设F₁、F₂是椭圆的两个焦点，点F₁、F₂到直线的距离分别为d₁、d₂，试求d₁·d₂的值，并判断直线L与椭圆M的位置关系。

（2）设F₁、F₂是椭圆的两个焦点，点F₁、F₂到直线（m、n不同时为0）的距离分别为d₁、d₂，且直线L与椭圆M相切，试求d₁·d₂的值。

（3）试写出一个能判断直线与椭圆的位置关系的充要条件，并证明。

（4）将（3）中得出的结论类比到其它曲线，请同学们给出自己研究的有关结论（不必证明）。

设F₁，F₂是椭圆的两个焦点，以F₁为圆心，且过椭圆中心的圆与椭圆的一个交点为M，若直线F₂M与圆F₁相切，则该椭圆的离心率是

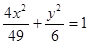设F₁，F₂是椭圆的两个焦点，P是椭圆上的点，且，

则的面积为（）

A．4 B．6 C． D．