题目内容
已知点 和
和 求过点
求过点 且与
且与 的距离相等的直线方程.
的距离相等的直线方程.
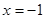 或
或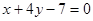
解析试题分析:由题可知,当过点C的直线斜率不存在时,点A、B到直线的距离相等;当直线斜率存在时,则与AB所在直线的斜率相等时,点A、B到直线的距离相等,故分两种情况求解.
试题解析:由题可知,当过点C的直线斜率不存在时,即直线为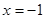 时,点A、B到直线的距离均为4;当直线斜率存在时,可知要使点A、B到直线的距离相等,则过点C的直线的斜率
时,点A、B到直线的距离均为4;当直线斜率存在时,可知要使点A、B到直线的距离相等,则过点C的直线的斜率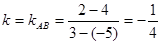 ,故此时直线方程为
,故此时直线方程为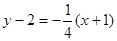 ,即
,即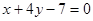 .
.
综上述,所求直线方程为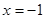 或
或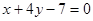 .
.
考点:1.点到直线的距离;2.直线的方程;3.两平行直线的距离.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 经过直线
经过直线 与直线
与直线 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
.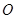 对称的直线方程.
对称的直线方程. 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,
, 的顶点
的顶点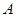 的坐标为
的坐标为 ,
, 边上的中线所在直线方程为
边上的中线所在直线方程为 的平分线所在直线方程为
的平分线所在直线方程为 ,求
,求 边所在直线的方程。
边所在直线的方程。 :
: ,
, :
: .
. ,求实数
,求实数 的值;(2)当
的值;(2)当 时,求直线
时,求直线 经过两点P1(4,-2)和P2(-1,8)。
经过两点P1(4,-2)和P2(-1,8)。 过点
过点 .
. 、
、 的距离相等时,求直线
的距离相等时,求直线 轴、
轴、 轴围成的三角形的面积为
轴围成的三角形的面积为 时,求直线
时,求直线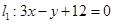 ,
, .求
.求 和
和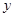 轴所围成的三角形面积.
轴所围成的三角形面积.