题目内容
【题目】已知三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在棱
在棱![]() 上,满足
上,满足![]() .
.
![]() 若
若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
![]() 设平面
设平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,若
,若![]() ,试判断命题“
,试判断命题“![]() ”的真假,并说明理由.
”的真假,并说明理由.
【答案】![]() 证明见解析
证明见解析 ![]() 假命题,理由见解析
假命题,理由见解析
【解析】
![]() 根据题意,设
根据题意,设![]() ,以点
,以点![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴,过
轴,过![]() 和
和![]() 平行的直线为
平行的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 建立空间直角坐标系,求平面
建立空间直角坐标系,求平面![]() 的一个法向量
的一个法向量![]() ,只需证明
,只需证明![]() ,即可得出结论成立;
,即可得出结论成立;
![]() 根据
根据![]() 中建立的坐标系,分别求出平面
中建立的坐标系,分别求出平面![]() 与平面
与平面![]() 的法向量,表示出两向量的夹角,根据题意,即可求出结果.
的法向量,表示出两向量的夹角,根据题意,即可求出结果.
![]() 因为
因为![]() ,设
,设![]() ,则
,则![]()
![]() ,所以
,所以![]() ,
,![]() ,以点
,以点![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴,过
轴,过![]() 和
和![]() 平行的直线为
平行的直线为![]() 轴,以
轴,以![]() 所在的直线为
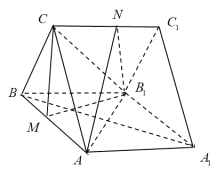
所在的直线为![]() 建立如图所示的空间直角坐标系,
建立如图所示的空间直角坐标系,
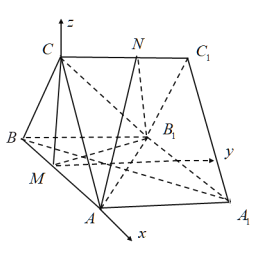
所以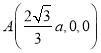 ,
,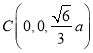
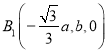 ,
,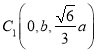
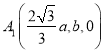 ,
,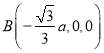
所以![]() ,
,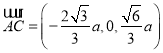 ,
,
所以![]() ,所以
,所以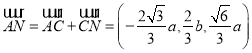 ,
,
![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则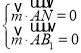
即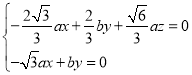 ,取
,取![]() ,则
,则![]() ,
,
所以![]() ,而
,而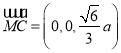 ,所以
,所以![]() ,
,
又因为直线![]() 在平面
在平面![]() 外,
外,
所以![]() 平面
平面![]() .
.
![]() 由
由![]() 可知,
可知,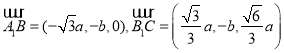 ,
,
因为![]() ,所以
,所以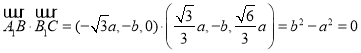 .
.
所以![]() ,
,
所以![]() ,所以
,所以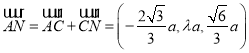 ,
,
![]() ,设
,设![]() 为平面
为平面![]() 的法向量.
的法向量.
则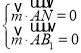 ,即
,即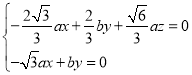 ,
,
取![]() ,则
,则![]() ,
,
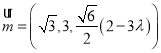 ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() 与
与![]() 的法向量
的法向量![]() 平行,
平行,
取![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
所以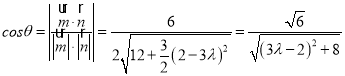
对于![]() ,若把
,若把![]() 看作
看作![]() 的函数.
的函数.
则此函数在![]() 上是单调递增的,在
上是单调递增的,在![]() 是单调递减的,
是单调递减的,
所以![]() ,所以
,所以![]() ,
,
所以不存在![]() ,使得
,使得![]() ,
,
命题“![]() ”是假命题.
”是假命题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目