题目内容
【题目】椭圆与双曲线有相同的焦点F1（﹣c，0），F2（c，0），椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行，若椭圆与双曲线的离心率分别为e1 ， e2 ， 则3e12+e22的最小值为 ．
【答案】
【解析】解：由题意可知：双曲线的焦点在x轴上，设椭圆的长轴为2a，短轴为2b，双曲线的实轴为2a'，虚轴为2b'，
∵椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行，
∴ 
= 
，即 
= ，
平方可得： 
= 
，由此得到 
= 即 
= ，
∴（ 
）2=（ 
）2 ，
由e1= ，e2= ，
∴e1e2=1，
∵e1、e2都是正数，
∴3e12+e22＞2 
=2 
，
当且仅当3e12=e22 ， 即e2= e1 ， e1= 
，e2= 时，等号成立，
∴3e12+e22的最小值 ，
所以答案是： ．
练习册系列答案
相关题目
【题目】为了解某地区某种农产品的年产量x（单位：吨）对价格y（单位：千元/吨）和利润z的影响，对近五年该农产品的年产量和价格统计如表：
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
（Ⅰ）求y关于x的线性回归方程 
；
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式： 
= 
= 
， 
．
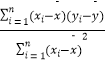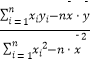【题目】已知 
x | |||||
2x+ | |||||
sin（2x+ | |||||
f（x） |
（1）用五点法完成下列表格，并画出函数f（x）在区间 
上的简图；
（2）若 
，函数g（x）=f（x）+m的最小值为2，试求处函数g（x）的最大值，指出x取值时，函数g（x）取得最大值．
