题目内容
已知函数f(x)是(-∞,+∞)上的偶函数,且f(5+x)=f(5-x),在[0,5]上只有f(1)=0,则f(x)在[-2 012,2 012]上的零点个数为( )
| A.804 | B.805 | C.806 | D.808 |
C
解析

练习册系列答案
相关题目
若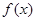 是偶函数,且当
是偶函数,且当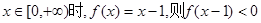 的解集是 ( )
的解集是 ( )
A. | B. | C. | D.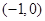 |
已知函数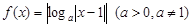 ,若
,若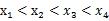 ,
,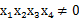
且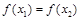
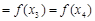 ,则
,则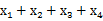 =( )
=( )
| A.2 | B.4 | C.8 | D.随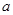 值变化 值变化 |
(2013•重庆)若a<b<c,则函数f(x)=(x﹣a)(x﹣b)+(x﹣b)(x﹣c)+(x﹣c)(x﹣a)的两个零点分别位于区间( )
| A.(a,b)和(b,c)内 | B.(﹣∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 | D.(﹣∞,a)和(c,+∞)内 |
已知函数y=ax2+bx+c(a≠0)的图象经过(-1,3)和(1,1)两点,若0<c<1,则a的取值范围是 ( )
| A.(1,3) | B.(1,2) |
| C.[2,3) | D.[1,3] |
下列函数为偶函数的是
| A.y=sinx | B.y=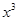 | C.y=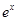 | D.y=ln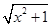 |
设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是( )
| A.f(x)+|g(x)|是偶函数 |
| B.f(x)-|g(x)|是奇函数 |
| C.|f(x)|+g(x)是偶函数 |
| D.|f(x)|-g(x)是奇函数 |
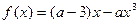 在区间[0,1]上的最小值等于-3,则实数
在区间[0,1]上的最小值等于-3,则实数 的取值范围是 ( )
的取值范围是 ( )