题目内容
(本小题共12分) 给定函数 和
和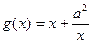
(I)求证: 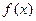 总有两个极值点;
总有两个极值点;
(II) 若
若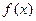 和
和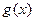 有相同的极值点,求
有相同的极值点,求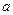 的值.
的值.
证明: (I)因为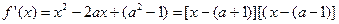 ,
,
令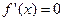 ,则
,则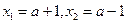 ,---------------------2分
,---------------------2分
则当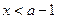 时,
时, 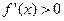 ,当
,当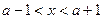 ,
, 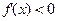
所以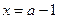 为
为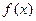 的一个极大值点, ------------4分
的一个极大值点, ------------4分
同理可证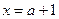 为
为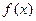 的一个极小值点.----- ----------5分
的一个极小值点.----- ----------5分
另解:(I)因为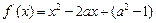 是一个二次函数,
是一个二次函数,
且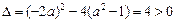 ,-------------------------------------2分
,-------------------------------------2分
所以导函数有两个不同的零点, 又因为导函数是一个二次函数,
又因为导函数是一个二次函数,
所以函数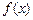 有两个不同的极值点.-------- ----------5分
有两个不同的极值点.-------- ----------5分
(II) 因为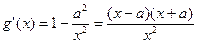 ,
,
令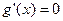 ,则
,则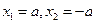 ---------------6分
---------------6分
因为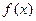 和
和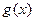 有相同的极值点, 且
有相同的极值点, 且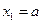 和
和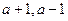 不可能相等,
不可能相等,
所以当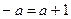 时,
时,  , 当
, 当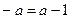 时,
时, 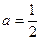 ,
,
经检验,  和
和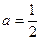 时,
时, 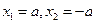 都是
都是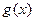 的极值点
的极值点
解析

练习册系列答案
相关题目
 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有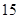 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个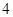 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.