题目内容
(本小题满分14分)
设函数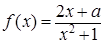 ,函数g(x)=
,函数g(x)=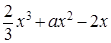 分别在x=m和x=n处取得极值,且
分别在x=m和x=n处取得极值,且
m<n
(1)求 的值
的值
(2)求证:f(x)在区间[m,n]上是增函数
(3)设f(x)在区间[m,n]上的最大值和最小值分别为M和N,试问当实数a为何值时,M-N取得最小值?并求出这个最小值
设函数
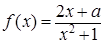 ,函数g(x)=
,函数g(x)=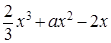 分别在x=m和x=n处取得极值,且
分别在x=m和x=n处取得极值,且m<n
(1)求
 的值
的值(2)求证:f(x)在区间[m,n]上是增函数
(3)设f(x)在区间[m,n]上的最大值和最小值分别为M和N,试问当实数a为何值时,M-N取得最小值?并求出这个最小值
解:(1)
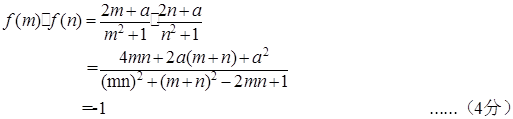
(2)f(x)在区间[m,n]上为增函数 ;
(3)a=0,f(n)=1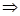 a="0"
a="0" 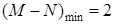 。
。
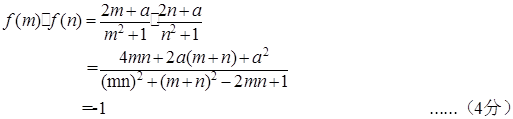
(2)f(x)在区间[m,n]上为增函数 ;
(3)a=0,f(n)=1
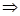 a="0"
a="0" 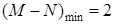 。
。本试题主要是考查了导数在研究函数中的运用求解函数的极值和函数的最值,以及函数的单调性问题的综合运用。
(1)因为为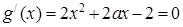 的两根为m,n
的两根为m,n
所以由韦达定理得 m+n=-a,mn=-1,从而解得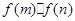 。
。
(2)运用导数的工具性作用,判定函数在给定区间的导数是否恒大于等于零得到。
(3)根据由(2)可知M=f(n),N=f(m)
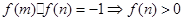
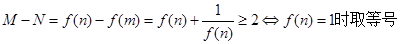
必有f(m)+f(n)=0,得到2mn(m+n)+2a="0" 所以a=0。
解:(1)因为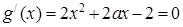 的两根为m,n
的两根为m,n
所以由韦达定理得 m+n=-a,mn=-1 ……(1分)
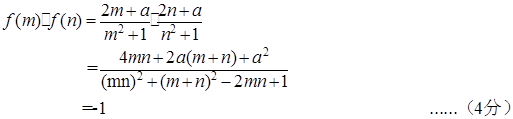
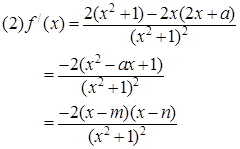
因为m≤x≤n,所以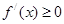
因此f(x)在区间[m,n]上为增函数 ……(8分)
(3)由(2)可知M=f(n),N=f(m)
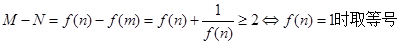 ……(10分)
……(10分)
必有f(m)+f(n)=0
又f(m)+f(n)=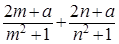
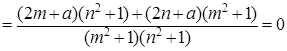
整理可得 2mn(m+n)+2a="0" 所以a=0
又可验证此时f(n)=1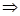 a="0"
a="0" 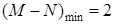 ……(14分)
……(14分)
(1)因为为
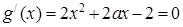 的两根为m,n
的两根为m,n所以由韦达定理得 m+n=-a,mn=-1,从而解得
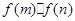 。
。(2)运用导数的工具性作用,判定函数在给定区间的导数是否恒大于等于零得到。
(3)根据由(2)可知M=f(n),N=f(m)
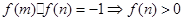
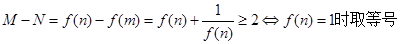
必有f(m)+f(n)=0,得到2mn(m+n)+2a="0" 所以a=0。
解:(1)因为
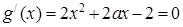 的两根为m,n
的两根为m,n所以由韦达定理得 m+n=-a,mn=-1 ……(1分)
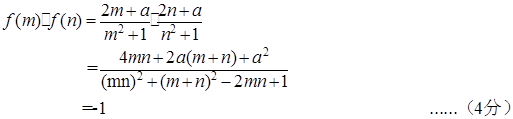
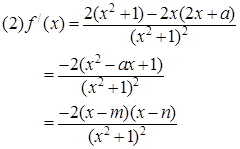
因为m≤x≤n,所以
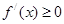
因此f(x)在区间[m,n]上为增函数 ……(8分)
(3)由(2)可知M=f(n),N=f(m)
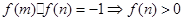
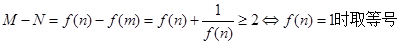 ……(10分)
……(10分)必有f(m)+f(n)=0
又f(m)+f(n)=
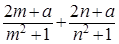
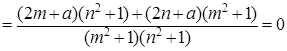
整理可得 2mn(m+n)+2a="0" 所以a=0
又可验证此时f(n)=1
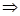 a="0"
a="0" 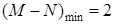 ……(14分)
……(14分)
练习册系列答案
相关题目
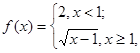
 则
则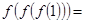 ( )
( )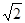
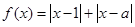
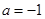 ,解不等式
,解不等式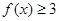 ;
;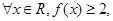 求a的取值范围.
求a的取值范围.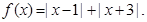
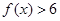 ;
;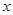 的不等式
的不等式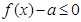 有解,求实数
有解,求实数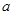 的取值范围.
的取值范围.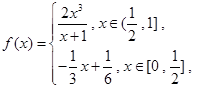 函数
函数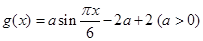 ,若存
,若存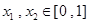 ,使得
,使得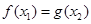 成立,则实数a的取值范围是 。
成立,则实数a的取值范围是 。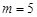 时,求f(x) >0的解集;
时,求f(x) >0的解集;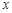 的不等式f(x) ≥2的解集是
的不等式f(x) ≥2的解集是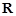 ,求
,求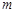 的取值范围
的取值范围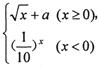 在R上连续,则实数a的值为
在R上连续,则实数a的值为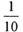
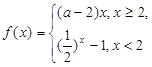 是R上的单调递减函数,则实数
是R上的单调递减函数,则实数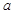 的取值范围是
的取值范围是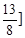
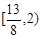
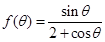 ,则
,则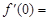 .
.