题目内容
已知函数f(x)=|x+1|+|x﹣2|﹣m
(I)当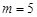 时,求f(x) >0的解集;
时,求f(x) >0的解集;
(II)若关于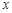 的不等式f(x) ≥2的解集是
的不等式f(x) ≥2的解集是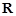 ,求
,求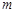 的取值范围
的取值范围
(I)当
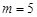 时,求f(x) >0的解集;
时,求f(x) >0的解集;(II)若关于
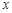 的不等式f(x) ≥2的解集是
的不等式f(x) ≥2的解集是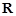 ,求
,求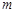 的取值范围
的取值范围(I)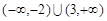 ; (II)
; (II)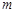 的取值范围是
的取值范围是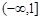 .
.
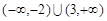 ; (II)
; (II)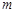 的取值范围是
的取值范围是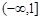 .
. 本试题主要是考查了绝对值不等式的求解和不等式恒成立的参数的取值范围的综合运用。
(1)利用三段论的思想分别进行求解不等式的解集,最后取其并集
(2)因为∵对于一切的实数,恒有|x+1|+|x﹣2|》3,故有不等式|x+1|+|x﹣2|》m解集是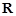 ,说明了m+2《3,可以得到参数的范围。
,说明了m+2《3,可以得到参数的范围。
解:(I)由题设知: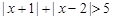 ,
,
不等式的解集是以下三个不等式组解集的并集:
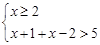 ,或
,或 ,或
,或 ,
,
解得函数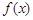 的定义域为
的定义域为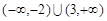 ; ……(5分)
; ……(5分)
(II)不等式f(x) ≥2即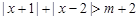 ,∵
,∵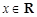 时,恒有
时,恒有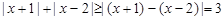 , 不等式
, 不等式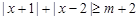 解集是
解集是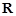 ,
,
∴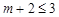 ,
,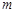 的取值范围是
的取值范围是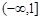 .
.
(1)利用三段论的思想分别进行求解不等式的解集,最后取其并集
(2)因为∵对于一切的实数,恒有|x+1|+|x﹣2|》3,故有不等式|x+1|+|x﹣2|》m解集是
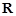 ,说明了m+2《3,可以得到参数的范围。
,说明了m+2《3,可以得到参数的范围。解:(I)由题设知:
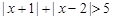 ,
,不等式的解集是以下三个不等式组解集的并集:
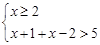 ,或
,或 ,或
,或 ,
,解得函数
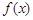 的定义域为
的定义域为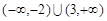 ; ……(5分)
; ……(5分)(II)不等式f(x) ≥2即
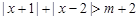 ,∵
,∵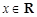 时,恒有
时,恒有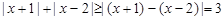 , 不等式
, 不等式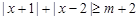 解集是
解集是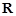 ,
,∴
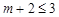 ,
,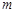 的取值范围是
的取值范围是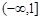 .
.
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
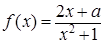 ,函数g(x)=
,函数g(x)=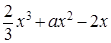 分别在x=m和x=n处取得极值,且
分别在x=m和x=n处取得极值,且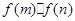 的值
的值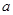 为实数,函数
为实数,函数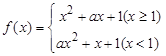 ,则“
,则“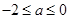 ”是“
”是“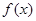 在
在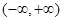 上是增函数”的( )
上是增函数”的( )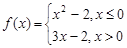 ,若
,若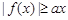 在
在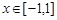 上恒成立,则实数
上恒成立,则实数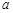 的取值范围是( )
的取值范围是( )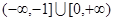
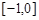
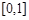
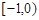
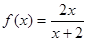 ,若
,若 ,则
,则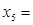 ______.
______.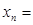 ______.
______. 若
若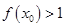 ,则
,则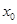 的取值范围是 .
的取值范围是 .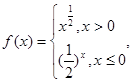 则
则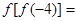
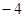
 ,则
,则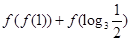 的值是( )
的值是( )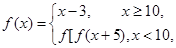 则
则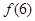 的值为
的值为