题目内容
过点O（0，0）引圆C：（x-2）2+（y-2）2=1的两条切线OA，OB，A，B为切点，则直线AB的方程是
2x+2y-7=0
2x+2y-7=0
．分析：设圆C：（x-2）2+（y-2）2=1的圆心M（2，2），先求出以OM为直径的圆，然后把该圆的方程与已知方程相减可得AB的方程
解答：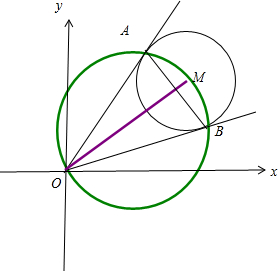
解设圆C：（x-2）2+（y-2）2=1的圆心M（2，2），连接OM
则AM⊥AO，OB⊥BM
∴以AM为直径的圆（x-1）2+（y-1）2=2经过点A，B即AB为两圆的公共弦
把两圆的方程相减可得2x+2y-7=0即AB的方程为2x+2y-7=0
故答案为：2x+2y-7=0
解设圆C：（x-2）2+（y-2）2=1的圆心M（2，2），连接OM则AM⊥AO，OB⊥BM
∴以AM为直径的圆（x-1）2+（y-1）2=2经过点A，B即AB为两圆的公共弦
把两圆的方程相减可得2x+2y-7=0即AB的方程为2x+2y-7=0
故答案为：2x+2y-7=0
点评：本题主要考查了直线与圆相切的 性质的应用，圆的方程的求解，两用公共弦的求解，属于知识的灵活应用
练习册系列答案
相关题目
已知抛物线C的顶点为O（0，0），焦点为F（0，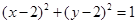
的两条切线OA,OB，A,B为切点，则直线AB的方程是______________．
=1(a＞b＞0)的离心率为
，短轴一
的两条切线PA、PB，A、B分别为切点，试探究椭圆C上是否存在点P，由点P向圆O所引的两条切线互相垂直？若存在，请求出点P的坐标；若不存在，请说明理由.