Question

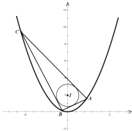已知抛物线C的顶点为O（0，0），焦点为F（0，

1

4

）．
（Ⅰ）求抛物线C的标准方程；
（Ⅱ）过抛物线C上的任意一点A（异于原点）向圆I：x²+（y-2）²=r²（0＜r＜1.2）引两条切线AB、AC，交抛物线于点B、C两点，若恒有直线BC与圆I相切，求圆I的半径r的值．

Answer 1

分析：（I）由抛物线的标准方程与基本概念，结合题中数据加以计算，可得抛物线C的方程为x²=y；
（II）设A（x₁，x12）、B（x₂，x22）、C（x₃，x32），其中x_i≠0且x_i≠±r（i=1，2，3）且横坐标互不相等．求出直线AB、AC、BC的方程，根据AB与圆I相切利用点到直线的距离公式列式并化简，算出x₂、x₃是一元二次方程（x₁²-r²）x²+（4-2r²）x₁x+4-r²-r²x12=0的两个根．利用根与系数的关系得到用x₁、r²表示x₂+x₃和x₂x₃的式子．由BC与圆I相切得

|2+x3x2|

(x3+x2)2+1

=r，代入前面求出的式子化简得r²x₁⁴+r²（4r⁴-18r²+16）x₁²+r⁶=（2-r²）²x₁⁴+2（4-3r²）（2-r²）x₁²+（4-3r²）²，再采用比较系数法建立关于r²的等式，解之可得r的值．

解答：解：（Ⅰ） 根据题意，设抛物线C的标准方程为x²=2py，
∵焦点为F（0，

1

4

），得

p

2

=

1

4

，
∴2p=1．可得抛物线C的标准方程为x²=y．
（Ⅱ）设A（x₁，x12），B（x₂，x22），C（x₃，x32），
其中x_i≠0，x_i≠±r且横坐标互不相等，（i=1，2，3），
则AB的斜率k_AB=

x12-x22

x1-x2

=x₁+x₂，得直线AB的方程为：y-x12=（x₁+x₂）（x-x₁），
化简得（x₁+x₂）x-y-x₁x₂=0，
同理可得直线AC的方程为（x₁+x₃）x-y-x₁x₃=0，直线BC的方程为（x₂+x₃）x-y-x₂x₃=0．
∵直线AB与圆I相切相切，∴圆心到AB的距离等于圆I的半径，即

|2+x1x2|

(x1+x2)2+1

=r，
化简得（x₁²-r²）x22+（4-2r²）x₁x₂+4-r²-r²x12=0，同理得（x₁²-r²）x32+（4-2r²）x₁x₃+4-r²-r²x12=0，
∴x₂、x₃是一元二次方程（x₁²-r²）x²+（4-2r²）x₁x+4-r²-r²x12=0的两个根．
可得x₂+x₃=

x1(2r2-4)

x12-r2

，x₂x₃=

-r2+4-r2x12

x12-r2

由直线BC与圆I相切，得

|2+x3x2|

(x3+x2)2+1

=r，代入上式化简，
得r²x₁⁴+r²（4r⁴-18r²+16）x₁²+r⁶=（2-r²）²x₁⁴+2（4-3r²）（2-r²）x₁²+（4-3r²）²，
由x₁的任意性，可知若上式恒成立，必须有

r2=(2-r2)2 r2(4r 4-18r2+16)=2(4-3r2)(2-r2) r6=(4-3r2)2 0＜r＜1.2

，解之得r=1．

点评：本题给出抛物线满足的条件，求抛物线的方程，并依此求△ABC的内切圆半径．着重考查了抛物线的标准方程与简单几何性质、点到直线的距离公式和直线与圆的位置关系等知识，属于中档题．