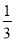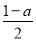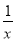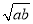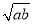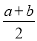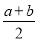题目内容
设函数f(x)=x3-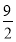 x2+6x-a.
x2+6x-a.
(1)对于任意实数x,f′(x)≥m恒成立,求m的最大值;
(2)若方程f(x)=0有且仅有一个实根,求a的取值范围.
(1)-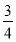 (2)(-∞,2)∪
(2)(-∞,2)∪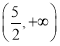
【解析】(1)f′(x)=3x2-9x+6,
因为x∈R时,f′(x)≥m,
即3x2-9x+(6-m)≥0恒成立,
所以Δ=81-12(6-m)≤0,得m≤-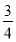 ,
,
故m的最大值为-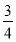 .
.
(2)由(1)知,f′(x)=3(x-1)(x-2),当x<1时,f′(x)>0;
当1<x<2时,f′(x)<0;当x>2时,f′(x)>0.
所以当x=1时,f(x)取极大值f(1)=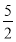 -a;
-a;
当x=2时,f(x)取极小值f(2)=2-a;
故当f(2)>0或f(1)<0时,方程f(x)=0仅有一个实根.
解得a<2或a>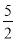 .
.
∴ 实数a的取值范围是(-∞,2)∪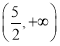 .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目