题目内容
在四棱锥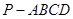 中,
中,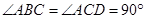 ,
,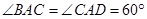 ,
,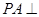 面
面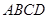 ,
,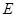 为
为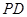 的中点,
的中点,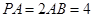 .
.

(1)求证: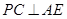 ;
;
(2)求证: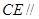 面
面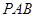 ;
;
(3)求三棱锥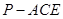 的体积
的体积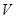 .
.
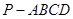 中,
中,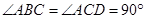 ,
,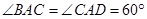 ,
,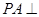 面
面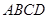 ,
,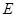 为
为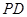 的中点,
的中点,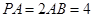 .
.
(1)求证:
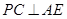 ;
;(2)求证:
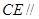 面
面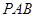 ;
;(3)求三棱锥
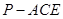 的体积
的体积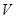 .
.((1)因为等腰三角形 中
中  ,同时
,同时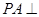 面
面 ,可知结论,
,可知结论,
(2)利用中位线性质在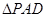 中,
中,  ∥
∥ .得到结论。
.得到结论。
(3)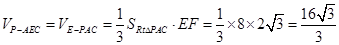
 中
中  ,同时
,同时 面
面 ,可知结论,
,可知结论,(2)利用中位线性质在
 中,
中,  ∥
∥ .得到结论。
.得到结论。(3)
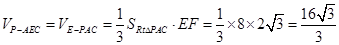
试题分析:解:(1)证明 取
 中点
中点 ,连接
,连接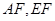 . 1分
. 1分 在
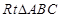 中,
中, ,
, ,
,则
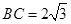 ,
, .
.而

则 在等腰三角形
 中
中  . ① 2分
. ① 2分又 在
 中,
中, ,
, 则
 ∥
∥ 3分
3分因
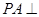 面
面 ,
, 面
面 ,
,则
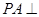
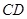 ,
,又
 ,即
,即 ,
,则
 面
面 , 4分
, 4分 ,
,所以
 . ② 5分
. ② 5分由①②知
 面
面 .
.故

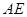 . 6分
. 6分 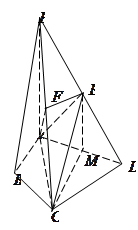
(2)(法一)取
 中点
中点 ,连接
,连接 .
.则 在
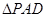 中,
中,  ∥
∥ .
.又
 面
面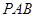 ,
,  面
面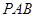
则
 ∥面
∥面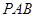 , 7分
, 7分在
 中,
中,
所以
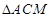 为正三角形,
为正三角形,则
 8分
8分又

则
 ∥
∥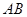 .
. 又
 面
面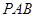 ,
,  面
面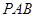
则
 ∥面
∥面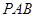 , 9分
, 9分而
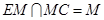 ,
,所以 面
 ∥面
∥面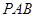 . 10分
. 10分又
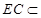 面
面
则
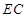 ∥面
∥面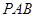 . 11分
. 11分(法二)延长
 交于
交于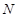 ,连接
,连接 . 7分
. 7分在
 中,
中, ,
,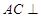
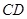 ,
,则
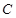 为
为 的中点 9分
的中点 9分又

所以
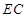 ∥
∥ 10分
10分又
 面
面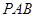 ,
,  面
面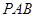
则
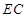 ∥面
∥面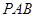 . 11分
. 11分(3)由(1)(2)知
 ,
, 

因
 面
面 ,
,  ∥
∥
则
 面
面 , 12分
, 12分故
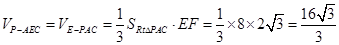 14分
14分点评:主要是考查了空间中线面的位置关系的判定以及体积的求解,属于中档题。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
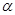 ,
,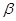 ,
,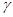 和直线
和直线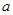 ,
,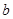 ,
,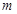 ,
,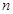 ,下列命题中真命题是 ( )
,下列命题中真命题是 ( ) ,则
,则 ;
; 则
则 ;
;  ,则
,则 ;
; ,则
,则 .
.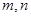 为不同的直线,
为不同的直线,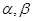 为不同的平面,给出下列四个命题:
为不同的平面,给出下列四个命题: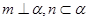 ,则
,则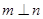 ; ②若
; ②若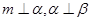 ,则
,则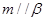 ;
;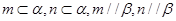 ,则
,则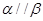 ; ④若
; ④若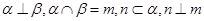 ,则
,则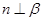 .
. 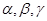 是三个不同的平 面,则下列为假命题的是
是三个不同的平 面,则下列为假命题的是 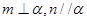 ,则
,则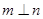



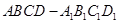 中,
中,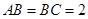 ,
,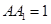 则
则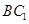 与平面
与平面 所成角的正弦值为 ( )
所成角的正弦值为 ( )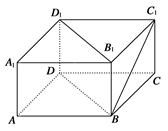




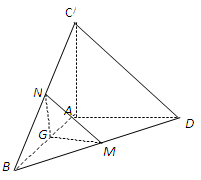
 是等边三角形,
是等边三角形, 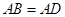 ,
,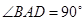 ,
, ,
, ,
, 分别是
分别是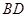 ,
,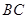 ,
,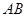 的中点,将△
的中点,将△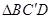 的位置,使得
的位置,使得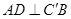 .
.
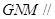 平面
平面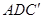 ;
;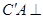 平面
平面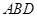 .
.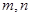 是两条不同的直线,
是两条不同的直线,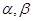 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )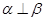 ,
, ,
, ,则
,则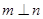
 ,
,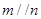
 ,
, ,则
,则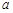 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,是下列命题中正确的是( )
是两个不同的平面,是下列命题中正确的是( ) ,
, ,则
,则
 ,
,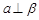
 ,
, ,
, ,则
,则