题目内容
已知正方体ABCD-A1B1C1D1，M是AA1的中点，N是BB1的中点．求证：面MDB1∥面ANC．
考点：平面与平面平行的判定
专题：空间位置关系与距离
分析：根据面面平行的判定定理即可证明．
解答：
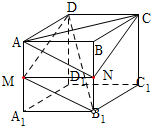证明：连结MN，∵M是AA1的中点，N是BB1的中点，
∴MN/CD，且MN=CD，
则四边形MNCD为平行四边形，
则DM∥CN，
又AM∥B1N，AM=B1N，
则四边形AMB1N为平行四边形，
∴AN∥MB1，
∵DM∩MB1=M，
∴面MDB1∥面ANC．
证明：连结MN，∵M是AA1的中点，N是BB1的中点，∴MN/CD，且MN=CD，
则四边形MNCD为平行四边形，
则DM∥CN，
又AM∥B1N，AM=B1N，
则四边形AMB1N为平行四边形，
∴AN∥MB1，
∵DM∩MB1=M，
∴面MDB1∥面ANC．
点评：本题主要考查面面平行的判断，根据面面平行的判定定理是解决本题的关键．
练习册系列答案
相关题目