题目内容
数列{an}的通项公式为an= (n∈N*),设f(n)=(1-a1)(1-a2)(1-a3)…(1-an).
(n∈N*),设f(n)=(1-a1)(1-a2)(1-a3)…(1-an).(1)求f(1)、f(2)、f(3)、f(4)的值;
(2)求f(n)的表达式;
(3)数列{bn}满足b1=1,bn+1=2f(n)-1,它的前n项和为g(n),求证:当n∈N*时,g(2n)-
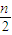 ≥1.
≥1.
【答案】分析:(1)直接利用数列{an}的通项公式为an=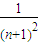 (n∈N*),分别令n=1,2,3,4.即可求得f(1)、f(2)、f(3)、f(4)的值;
(n∈N*),分别令n=1,2,3,4.即可求得f(1)、f(2)、f(3)、f(4)的值;
(2)由f(n)=(1-a1)(1-a2)…(1-an)得:f(n-1)=(1-a1)(1-a2)…(1-an-1)(n>1),两式相除得:
即可得出f(n)的表达式;
(3)先利用题中条件得出g(2n)=1+ +
+ +…+
+…+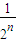 .再设∅(n)=f(2n)-
.再设∅(n)=f(2n)-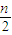 ,研究它的单调性,即数列{∅(n)}是单调递增数列,从而求得其最小值为∅(1),从而得到∅(n)≥1即得g(2n)-
,研究它的单调性,即数列{∅(n)}是单调递增数列,从而求得其最小值为∅(1),从而得到∅(n)≥1即得g(2n)-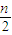 ≥1.
≥1.
解答:解:(1)f(1)= ,f(2)=
,f(2)= ,f(3)=
,f(3)= ,f(4)=
,f(4)=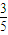 .
.
(2)由f(n)=(1-a1)(1-a2)…(1-an)
得:f(n-1)=(1-a1)(1-a2)…(1-an-1)(n>1),
两式相除得:
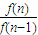 =1-an=1-
=1-an=1-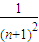 =
=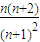 (n>1).
(n>1).
∴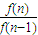
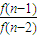 …
…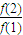 =
=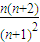
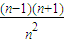
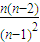 …
…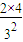 ,
,
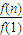 =
=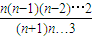 •
•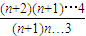 =
=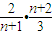 ,
,
∴f(n)=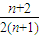 (n>1),又f(1)=
(n>1),又f(1)= 适合此式,
适合此式,
∴f(n)=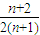 .
.
(3)b n+1=2f(n)-1=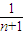 ,
,
g(n)=1+ +
+ +…+
+…+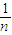 ,
,
∴g(2n)=1+ +
+ +…+
+…+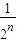 .
.
设∅(n)=f(2n)-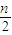 ,
,
则∅(n)=1+ +
+ +…+
+…+ .
.
∅(n+1)-∅(n)=1+ +
+ +…+
+…+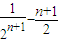 -(1+
-(1+ +
+ +…+
+…+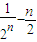 )
)
=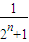 +
+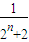 +…+
+…+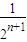 -
- .
.
∵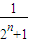 +
+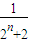 +…+
+…+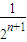 的项数为2n,
的项数为2n,
∴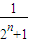 +
+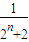 +…+
+…+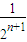 >
>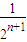 +
+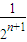 +…+
+…+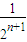 =
=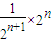 =
= ,
,
∴∅(n+1)-∅(n)>0.即数列{∅(n)}是单调递增数列.
其最小值为∅(1)=g(2)- =1
=1
∴∅(n)≥1即g(2n)-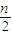 ≥1.
≥1.
点评:本小题主要考查函数单调性的应用、数列的函数特性、数列的求和、数列与不等式的综合等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
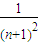 (n∈N*),分别令n=1,2,3,4.即可求得f(1)、f(2)、f(3)、f(4)的值;
(n∈N*),分别令n=1,2,3,4.即可求得f(1)、f(2)、f(3)、f(4)的值;(2)由f(n)=(1-a1)(1-a2)…(1-an)得:f(n-1)=(1-a1)(1-a2)…(1-an-1)(n>1),两式相除得:
即可得出f(n)的表达式;
(3)先利用题中条件得出g(2n)=1+
 +
+ +…+
+…+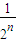 .再设∅(n)=f(2n)-
.再设∅(n)=f(2n)-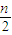 ,研究它的单调性,即数列{∅(n)}是单调递增数列,从而求得其最小值为∅(1),从而得到∅(n)≥1即得g(2n)-
,研究它的单调性,即数列{∅(n)}是单调递增数列,从而求得其最小值为∅(1),从而得到∅(n)≥1即得g(2n)-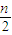 ≥1.
≥1.解答:解:(1)f(1)=
 ,f(2)=
,f(2)= ,f(3)=
,f(3)= ,f(4)=
,f(4)=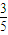 .
.(2)由f(n)=(1-a1)(1-a2)…(1-an)
得:f(n-1)=(1-a1)(1-a2)…(1-an-1)(n>1),
两式相除得:
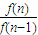 =1-an=1-
=1-an=1-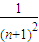 =
=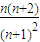 (n>1).
(n>1).∴
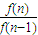
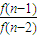 …
…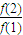 =
=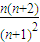
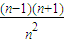
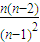 …
…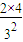 ,
,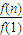 =
=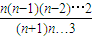 •
•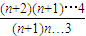 =
=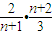 ,
,∴f(n)=
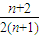 (n>1),又f(1)=
(n>1),又f(1)= 适合此式,
适合此式,∴f(n)=
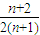 .
.(3)b n+1=2f(n)-1=
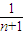 ,
,g(n)=1+
 +
+ +…+
+…+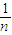 ,
,∴g(2n)=1+
 +
+ +…+
+…+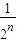 .
.设∅(n)=f(2n)-
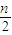 ,
,则∅(n)=1+
 +
+ +…+
+…+ .
.∅(n+1)-∅(n)=1+
 +
+ +…+
+…+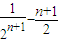 -(1+
-(1+ +
+ +…+
+…+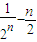 )
)=
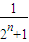 +
+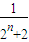 +…+
+…+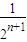 -
- .
.∵
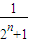 +
+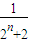 +…+
+…+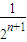 的项数为2n,
的项数为2n,∴
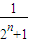 +
+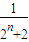 +…+
+…+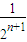 >
>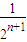 +
+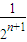 +…+
+…+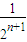 =
=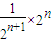 =
= ,
,∴∅(n+1)-∅(n)>0.即数列{∅(n)}是单调递增数列.
其最小值为∅(1)=g(2)-
 =1
=1∴∅(n)≥1即g(2n)-
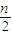 ≥1.
≥1.点评:本小题主要考查函数单调性的应用、数列的函数特性、数列的求和、数列与不等式的综合等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,Tn为数列{bn}的前n项和,求Tn.
,Tn为数列{bn}的前n项和,求Tn.