题目内容
【题目】在直四棱柱![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.
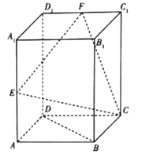
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,利用菱形对角线的性质得出
,利用菱形对角线的性质得出![]() ,由直棱柱的性质得出
,由直棱柱的性质得出![]() 平面
平面![]() ,可得出
,可得出![]() ,由直线与平面垂直的判定定理可证明出
,由直线与平面垂直的判定定理可证明出![]() 平面
平面![]() ,由此可证明出
,由此可证明出![]() ;
;
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 轴,过点
轴,过点![]() 垂直于平面
垂直于平面![]() 的直线为
的直线为![]() 轴,建立如图的空间直角坐标系
轴,建立如图的空间直角坐标系![]() ,然后利用空间向量法计算出平面
,然后利用空间向量法计算出平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)连接![]() ,交
,交![]() 于点
于点![]() .
.
因为四边形![]() 是菱形,所以
是菱形,所以![]() .
.
因为四棱柱![]() 是直四棱柱,所以
是直四棱柱,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ;
;
(2)由(1)知![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 轴,过点
轴,过点![]() 垂直于平面
垂直于平面![]() 的直线为
的直线为![]() 轴,建立如图的空间直角坐标系
轴,建立如图的空间直角坐标系![]() .
.
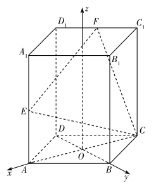
因为![]() ,所以
,所以![]() ,因为底面四边形
,因为底面四边形![]() 为菱形,且
为菱形,且![]() ,
,
所以![]() ,
,![]() ,又因为
,又因为![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,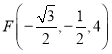 ,
,
所以![]() ,
,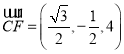 .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则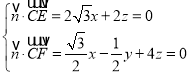 .
.
令![]() ,得
,得![]() .
.
易知![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,
,
所以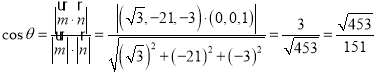 ,
,
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到频数分布表和频率分布直方图如下.
组号 | 分组 | 频数 |
1 | [0,2) | 6 |
2 | [2,4) | 8 |
3 | [4,6) | 17 |
4 | [6,8) | 22 |
5 | [8,10) | 25 |
6 | [10,12) | 12 |
7 | [12,14) | 6 |
8 | [14,16) | 2 |
9 | [16,18) | 2 |
合计 | 100 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率分布直方图中的a,b的值.