题目内容
11.在数列{an}中,已知a1=$\frac{1}{2}$,an=an-1+$\frac{1}{n(n+1)}$(n≥2,n∈N*)(1)计算a2,a3,a4的值,并归纳猜想出数列{an}的通项公式;
(2)利用公式$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$证明你的猜想.
分析 (1)由a1=$\frac{1}{2}$,an=an-1+$\frac{1}{n(n+1)}$,求得a2=$\frac{2}{3}$,a3=$\frac{3}{4}$,a4=$\frac{4}{5}$,从而猜想an=$\frac{n}{n+1}$;
(2)由an=an-1+$\frac{1}{n(n+1)}$可得an-an-1=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,从而利用叠加法求得.
解答 解:(1)∵a1=$\frac{1}{2}$,an=an-1+$\frac{1}{n(n+1)}$,
∴a2=a1+$\frac{1}{2×3}$=$\frac{1}{2}$+$\frac{1}{6}$=$\frac{2}{3}$,
a3=a2+$\frac{1}{12}$=$\frac{3}{4}$,
a4=a3+$\frac{1}{4×5}$=$\frac{4}{5}$,
故猜想an=$\frac{n}{n+1}$;
(2)证明:∵an=an-1+$\frac{1}{n(n+1)}$,a1=$\frac{1}{2}$;
∴a2-a1=$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,
a3-a2=$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,
…
an-an-1=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
将以上n-1个等式相加得,
an-a1=($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)=$\frac{1}{2}$-$\frac{1}{n+1}$,
∴an=a1+$\frac{1}{2}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
当n=1时也成立,
故an=$\frac{n}{n+1}$成立.
点评 本题考查了数列的应用及叠加法的应用,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 30 | B. | 40 | C. | 60 | D. | 120 |
| A. | 20 | B. | 19 | C. | 18 | D. | 16 |
| A. | $-\frac{12}{25}$ | B. | $\frac{7}{5}$ | C. | $\frac{1}{25}$ | D. | $-\frac{7}{25}$ |
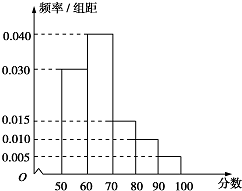 某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.
某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.