Question

【题目】已知函数f（x）= sin2x+cos2（ ﹣x）﹣ （x∈R）．
（1）求函数f（x）在区间[0， ]上的最大值；
（2）在△ABC中，若A＜B，且f（A）=f（B）= ，求 的值．

Answer 1

【答案】
（1）解：f（x）= sin2x+cos2（ ﹣x）﹣

= + ﹣

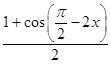= sin2x﹣ cos2x

=sin（2x﹣ ）

由于0≤x≤ ，因此﹣ ≤2x﹣ ≤ ，所以当2x﹣ = 即x= 时，f（x）取得最大值，最大值为1

（2）解：由已知，A、B是△ABC的内角，A＜B，且f（A）=f（B）= ，

可得：2A﹣ = ，2B﹣ = ，

解得A= ，B= ，

所以C=π﹣A﹣B= ，

得 =

【解析】（1）利用三角恒等变换的应用可化简f（x）=sin（2x﹣ ），再利用正弦函数的单调性可求函数f（x）在区间[0， ]上的最大值；（2）在△ABC中，由A＜B，且f（A）=f（B）= ，可求得A= ，B= ，再利用正弦定理即可求得 的值．
【考点精析】掌握三角函数的最值是解答本题的根本，需要知道函数，当时，取得最小值为；当时，取得最大值为，则，，．