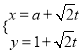题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当a=2时,求(x)在x∈[1,e2]时的最值(参考数据:e2≈7.4);
(Ⅱ)若![]() ,有f(x)+g(x)≤0恒成立,求实数a的值;
,有f(x)+g(x)≤0恒成立,求实数a的值;
【答案】(Ⅰ)f(x)max=2ln2,![]() ;(Ⅱ)a=1.
;(Ⅱ)a=1.
【解析】试题分析:
(1)利用导函数与原函数的单调性可得函数的最大值为f(x)max=f(2)=2ln2;
(2)构造新函数h(x)=f(x)+g(x)=alnx-x+1,利用函数的特征分类讨论可得a=1.
试题解析:
(Ⅰ)由于![]() ,∴
,∴![]() .
.
因此,函数f(x)在[1,2]为增函数,在[2,e2]为减函数.
所以f(x)max=f(2)=2ln2.
![]() .
.
(Ⅱ)令h(x)=f(x)+g(x)=alnx-x+1,则![]() ,
,
(1)当a≤0时,h(x)在(0,+∞)上为减函数,而h(1)=0,
∴h(x)≤0在区间x∈(0,+∞)上不可能恒成立,因此a≤0不满足条件.
(2)当a>0时,h(x)在(0,a)上递增,在(a,+∞)上递减,所以
h(x)max=h(a)=alna-a+1.
由于h(x)≤0在x∈(0,+∞)恒成立,则h(x)max≤0.即alna-a+1≤0.
令g(a)=alna-a+1,(a>0),则g'(a)=lna,∴g(a)在(0,1)上递减,在(1,+∞)上递增,∴g(a)min=g(1)=0,故a=1.

 阅读快车系列答案
阅读快车系列答案【题目】一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
频数 | 2 | 12 | 34 | 38 | 10 | 4 |
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.