题目内容
【题目】四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 平面
平面![]() .
.
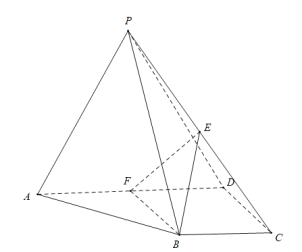
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)通过线面平行,推证出点![]() 的位置,再结合面面垂直,推证出
的位置,再结合面面垂直,推证出![]() 平面
平面![]() ,即可由线面垂直推证面面垂直;
,即可由线面垂直推证面面垂直;
(2)以![]() 点为坐标原点建立空间直角坐标系,由线面角求得
点为坐标原点建立空间直角坐标系,由线面角求得![]() 长度,进而再由向量法求得二面角的大小即可.
长度,进而再由向量法求得二面角的大小即可.
(1)连![]() 交
交![]() 于
于![]() ,连
,连![]() ,如下图所示:
,如下图所示:

因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() 为
为![]() 中点,
中点,
所以![]() 为
为![]() 中点,由
中点,由![]() ≌
≌![]() ,
,
∴![]()
∴![]() 为
为![]() 中点,
中点,
∵![]() ,且
,且![]() ,则
,则![]() 为平行四边形,
为平行四边形,
∵![]()
∴![]() ,又
,又![]() 平面
平面![]() ,
,
平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]()
![]() ,
,
故![]() ⊥平面
⊥平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() ⊥平面
⊥平面![]() .即证.
.即证.
(2)连接![]() ,
,
∵![]() ,
,![]() 为AD的中点,∴
为AD的中点,∴![]() ,
,
又![]() 平面
平面![]() ,平面
,平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]()
![]() ,
,
∴![]() 底面
底面![]() ,又
,又![]() ,
,
以![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
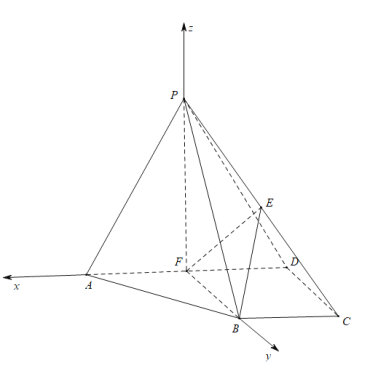
设![]() ,取平面
,取平面![]() 的法向量
的法向量![]() ,
,
又![]() ,
,![]()
∴
∴![]() ,
,![]()
设平面EBF的法向量![]() 所以
所以
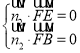 即可得
即可得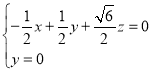
令![]()
设二面角![]() 的平面角为
的平面角为![]()
∴ ,又
,又![]() 为钝角
为钝角
∴![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某中学高三(3)班有学生50人,现调查该班学生每周平均体育锻炼时间的情况,得到如下频率分布直方图,其中数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
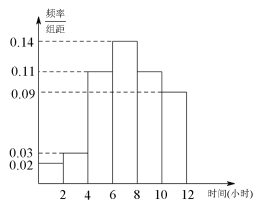
(1)从每周平均体育锻炼时间在![]() 的学生中,随机抽取2人进行调查,求这2人的每周平均体育锻炼时间都超过2小时的概率;
的学生中,随机抽取2人进行调查,求这2人的每周平均体育锻炼时间都超过2小时的概率;
(2)已知全班学生中有40%是女姓,其中恰有3个女生的每周平均体育锻炼时间不超过4小时,若每周平均体育锻炼时间超过4小时称为经常锻炼,问:有没有90%的把握说明,经常锻炼与否与性别有关?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某地计划在水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台发电机年净利润为5000万元;若某台发电机未运行,则该台发电机年维护费与年入流量![]() 有如下关系:
有如下关系:
年入流量 |
|
|
一台未运行发电机年维护费 | 500 | 800 |
欲使水电站年净利润最大,应安装发电机多少台?
