题目内容
某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且运费由厂商承担.若厂商恰能在约定日期(×月×日)将牛奶送到,则城市乙的销售商一次性支付给牛奶厂20万元;若在约定日期前送到,每提前一天销售商将多支付给牛奶厂1万元;若在约定日期后送到,每迟到一天销售商将少支付给牛奶厂1万元.为保证牛奶新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送牛奶,已知下表内的信息:
| 统计信息 汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 | 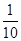 | 1.6 |
| 公路2 | 1 | 4 | 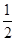 | 0.8 |
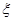 (单位:万元),求
(单位:万元),求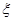 的分布列和数学期望
的分布列和数学期望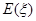 ;
;(II)如果你是牛奶厂的决策者,你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多?
(注:毛收入=销售商支付给牛奶厂的费用-运费)
(1)分布列详见解析, ;(2)选择公路2运送牛奶有可能让牛奶厂获得的毛收入更多.
;(2)选择公路2运送牛奶有可能让牛奶厂获得的毛收入更多.
解析试题分析:本题主要考查实际问题中的数学问题,考查离散型随机变量的分布列和数学期望.第一问,通过分析题意,有堵车和不堵车2种情况,分别求出这2种情况牛奶厂获得的毛收入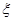 的值,列出分布列,用期望的计算公式计算出期望;第二问,第二问的情况和第一问一样,先求出走公路2时,毛收入
的值,列出分布列,用期望的计算公式计算出期望;第二问,第二问的情况和第一问一样,先求出走公路2时,毛收入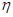 的期望,再比较2个期望
的期望,再比较2个期望 和
和 的大小.
的大小.
试题解析:(I)若汽车走公路1.
不堵车时牛奶厂获得的毛收入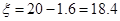 (万元);
(万元);
堵车时牛奶厂获得的毛收入 (万元). 2分
(万元). 2分
∴汽车走公路1时牛奶厂获得的毛收入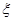 的分布列为
的分布列为
∴ξ 18.4 17.4 P 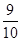
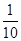
 (万元). 5分
(万元). 5分
(II)设汽车走公路2时牛奶厂获得的毛收入为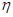 ,则
,则
不堵车时牛奶厂获得的毛收入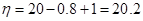 (万元);
(万元);
堵车时牛奶厂获得的毛收入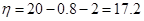 (万元). 7分
(万元). 7分
∴汽车走公路2时牛奶厂获得的毛收入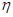 的分布列为
的分布列为η 20.2 17.2 P 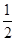
 (万元). 10分
(万元). 10分
∵ ,
,
∴选择公路2运送牛奶有可能让牛奶厂获得的毛收入更多. 12分
考点:离散型随机变量的分布列和数学期望.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望
 .
.  ,
,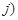 表示甲乙抽到的牌的数字,
表示甲乙抽到的牌的数字, 如甲抽到红桃2,乙抽到红桃3,记为
如甲抽到红桃2,乙抽到红桃3,记为 ,
,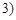 ,写出甲乙二人抽到的牌的所有情况;
,写出甲乙二人抽到的牌的所有情况; ,乙获胜的概率为
,乙获胜的概率为 ,现已赛完两局,乙暂时以2∶0领先.
,现已赛完两局,乙暂时以2∶0领先. ,
, ,点
,点 的坐标为
的坐标为 .
. 时,点
时,点 的概率;
的概率; 时,点
时,点
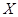 ,求随机变量
,求随机变量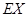 .
.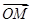 |2的所有取值之和;
|2的所有取值之和;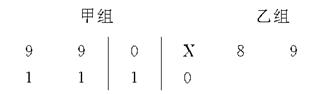
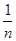 [(x1-
[(x1- )2+(x2-
)2+(x2-