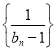题目内容
【题目】设函数![]() .(
.(![]() 且
且![]() )
)
(1)分别判断当![]() 及
及![]() 时函数的奇偶性;
时函数的奇偶性;
(2)在![]() 且
且![]() 的条件下,将(1)的结论加以推广,使命题(1)成为推广后命题的特例,并对推广的结论加以证明.
的条件下,将(1)的结论加以推广,使命题(1)成为推广后命题的特例,并对推广的结论加以证明.
【答案】(1)![]() 时,
时,![]() 既不是奇函数也不是偶函数,
既不是奇函数也不是偶函数,![]() 时,
时,![]() 是奇函数.;(2)
是奇函数.;(2)![]() 时,
时,![]() 既不是奇函数也不是偶函数,
既不是奇函数也不是偶函数,![]() 时,
时,![]() 是奇函数.证明见解析.
是奇函数.证明见解析.
【解析】
(1)根据奇偶性定义判断;
(2)![]() 时,
时,![]() 既不是奇函数也不是偶函数,
既不是奇函数也不是偶函数,![]() 时,
时,![]() 是奇函数.根据奇偶性定义证明即可.
是奇函数.根据奇偶性定义证明即可.
(1)![]() 时,
时, ,定义域为
,定义域为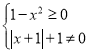 ,
,![]() ,
,
此时![]() ,
,![]() ,
,![]() 且
且![]() ,
,![]() 既不是奇函数也不是偶函数,
既不是奇函数也不是偶函数,
![]() 时,
时,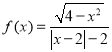 ,定义域为
,定义域为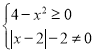 ,
,![]() 且
且![]() ,
,
此时![]() ,
,![]() ,
,![]() 是奇函数.
是奇函数.
(2)![]() 时,
时,![]() 既不是奇函数也不是偶函数,
既不是奇函数也不是偶函数,![]() 时,
时,![]() 是奇函数.
是奇函数.
与(1)类似,![]() 时,由
时,由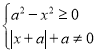 ,得函数定义域是
,得函数定义域是![]() ,
,![]() ,
,![]() 与
与![]() 既不相等也不是相反数,因此
既不相等也不是相反数,因此![]() 既不是奇函数也不是偶函数,
既不是奇函数也不是偶函数,
![]() 时,由
时,由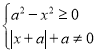 ,得定义域是
,得定义域是![]() ,
,![]() ,
,![]() ,
,![]() 是奇函数.
是奇函数.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
【题目】为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如表
评估的平均得分 | (0,6] | (6,8] | (8,10] |
全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级.
(2)用简单随机抽样方法从这6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超0.5的概率.