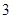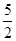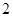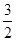题目内容
已知函数 ,
, .
.
(1)若曲线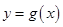 在点
在点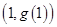 处的切线平行于
处的切线平行于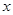 轴,求
轴,求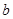 的值;
的值;
(2)当 时,若对
时,若对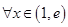 ,
,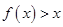 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)设 ,在(1)的条件下,证明当
,在(1)的条件下,证明当 时,对任意两个不相等的正数
时,对任意两个不相等的正数 、
、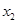 ,有
,有 .
.
 ,
, .
.(1)若曲线
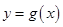 在点
在点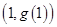 处的切线平行于
处的切线平行于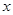 轴,求
轴,求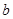 的值;
的值;(2)当
 时,若对
时,若对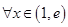 ,
,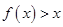 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)设
 ,在(1)的条件下,证明当
,在(1)的条件下,证明当 时,对任意两个不相等的正数
时,对任意两个不相等的正数 、
、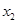 ,有
,有 .
.(1)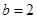 ;(2)
;(2)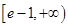 ;(3)详见解析.
;(3)详见解析.
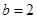 ;(2)
;(2)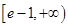 ;(3)详见解析.
;(3)详见解析.试题分析:(1)先求导
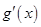 ,利用题中条件得到
,利用题中条件得到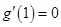 ,从而求出实数
,从而求出实数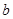 的值;(2)解法一是构造新函数
的值;(2)解法一是构造新函数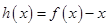 ,问题转化为
,问题转化为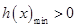 来处理,求出导数
来处理,求出导数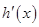 的根
的根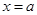 ,对
,对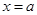 与区间
与区间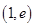 的相对位置进行分类讨论,以确定函数
的相对位置进行分类讨论,以确定函数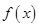 的单调性与最值,从而解决题中的问题;解法二是利用参数分离法将问题转化为
的单调性与最值,从而解决题中的问题;解法二是利用参数分离法将问题转化为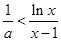 ,从而将问题转化为
,从而将问题转化为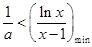 来处理,而将
来处理,而将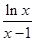 视为点
视为点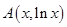 与点
与点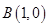 连线的斜率,然后利用图象确定
连线的斜率,然后利用图象确定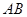 斜率的最小值,从而求解相应问题;(3)证法一是利用基本不等式证明
斜率的最小值,从而求解相应问题;(3)证法一是利用基本不等式证明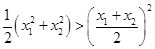 和
和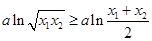 ,再将三个同向不等式相加即可得到问题的证明;证法二是利用作差法结合基本不等式得到
,再将三个同向不等式相加即可得到问题的证明;证法二是利用作差法结合基本不等式得到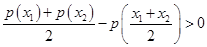 进而得到问题的证明.
进而得到问题的证明.试题解析:(1)
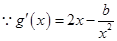 ,由曲线
,由曲线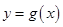 在点
在点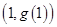 处的切线平行于
处的切线平行于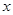 轴得
轴得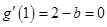 ,
,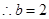 ;
;(2)解法一:当
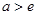 时,
时,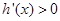 ,函数
,函数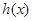 在
在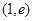 上是增函数,有
上是增函数,有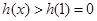 ,------6分
,------6分当
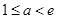 时,
时,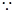 函数
函数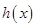 在
在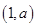 上递增,在
上递增,在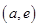 上递减,
上递减,对
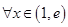 ,
,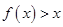 恒成立,只需
恒成立,只需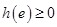 ,即
,即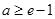 ;
;当
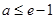 时,函数
时,函数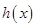 在
在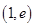 上递减,对
上递减,对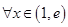 ,
,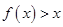 恒成立,只需
恒成立,只需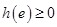 ,
,而
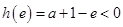 ,不合题意,
,不合题意,综上得对
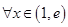 ,
,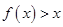 恒成立,
恒成立,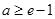 ;
;解法二:由
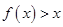 且
且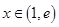 可得
可得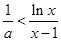 ,
,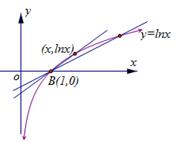
由于
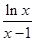 表示两点
表示两点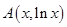 、
、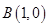 的连线斜率,
的连线斜率,由图象可知
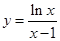 在
在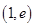 单调递减,
单调递减,故当
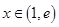 ,
,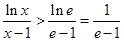 ,
,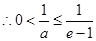 ,即
,即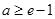 ;
;(3)证法一:由
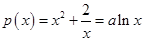 ,
,得
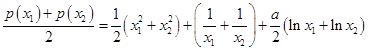
 ,
,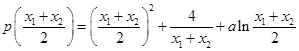 ,
,由
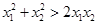 得
得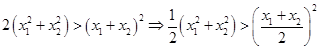 ,①
,①又
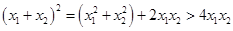 ,
,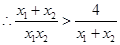 ,②
,②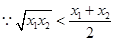 ,
,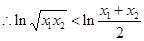 ,
,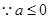 ,
,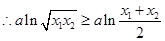 ,③
,③由①、②、③得
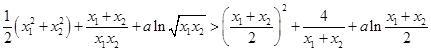 ;
;即
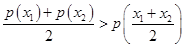 ;
;证法二:由
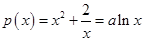
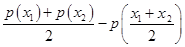
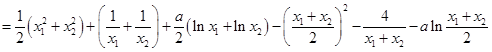
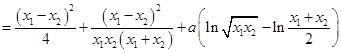
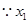 、
、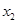 是两个不相等的正数,
是两个不相等的正数,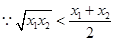 ,
,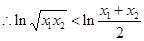 ,
,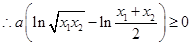 ,又
,又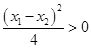 ,
,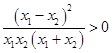 ,
,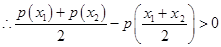 ,即
,即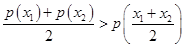

练习册系列答案
相关题目
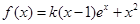 .
.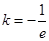 ,求函数
,求函数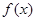 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;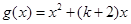 的图象恒在
的图象恒在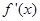 图象的上方,求k的取值范围;
图象的上方,求k的取值范围; .
. 在
在 处的切线方程;
处的切线方程; 时,求证:
时,求证: ;
; ,且
,且 对任意
对任意 恒成立,求k的最大值.
恒成立,求k的最大值.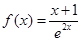 .
.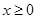 时,
时,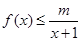 恒成立,求m的取值范围;
恒成立,求m的取值范围;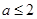 时,求证:
时,求证: .
. .
. 在点
在点 处的切线与直线
处的切线与直线 平行,求实数
平行,求实数 的值;
的值; 在
在 处取得极小值,且
处取得极小值,且 ,求实数
,求实数 的取值范围.
的取值范围.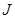 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算, (单位:
(单位: )与速度
)与速度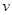 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.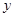 (元)(不计返程费用),将
(元)(不计返程费用),将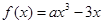 .
.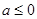 时,求函数
时,求函数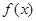 单调区间;
单调区间;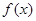 在区间[1,2]上的最小值为
在区间[1,2]上的最小值为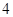 ,求
,求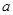 的值.
的值. 是R上的单调增函数,则
是R上的单调增函数,则 的取值范围是( )
的取值范围是( )



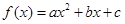 的导数为
的导数为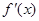 ,
,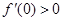 ,对于任意实数
,对于任意实数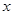 ,有
,有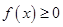 ,则
,则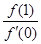 的最小值为( )
的最小值为( )