题目内容
设数列{an}的前n项积为Tn,已知对?n,m∈N+,当n>m时,总有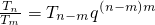 (q>0是常数).
(q>0是常数).
(1)求证:数列{an}是等比数列;
(2)设正整数k,m,n(k<m<n)成等差数列,试比较Tn•Tk和(Tm)2的大小,并说明理由;
(3)探究:命题p:“对?n,m∈N+,当n>m时,总有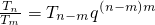 (q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件吗?若是,请给出证明;若不是,请说明理由.
(q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件吗?若是,请给出证明;若不是,请说明理由.
(1)证明:设m=1,则有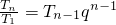 ,∴
,∴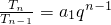
∴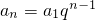
∴n≥2时,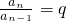
∴数列{an}是等比数列;
(2)解:当q=1时,an=a1,∴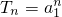 ,∴Tn•Tk=
,∴Tn•Tk=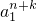 =
=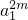 =
=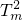
当q≠1时,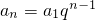 ,
,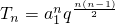
∴Tn•Tk=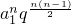 •
•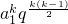 =
=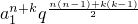
∵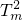 =
=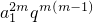 ,n+k=2m,k<m<n
,n+k=2m,k<m<n
∴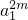 =
=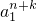 ,
,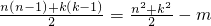 >
>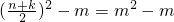
∴q>1时,Tn•Tk>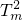 ;q<1时,Tn•Tk<
;q<1时,Tn•Tk<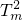
(3)证明:由(1)知,充分性成立;
必要性:若数列{an}是公比为q(q>0)的等比数列,则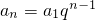
∴q≠1时,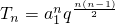
∴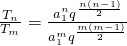 =
=
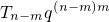 =
=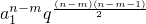 •q(n-m)m=
•q(n-m)m=
∴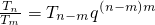
∴对?n,m∈N+,当n>m时,总有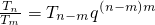 (q>0是常数)
(q>0是常数)
同理可证,当q=1时,也成立
∴命题p:“对?n,m∈N+,当n>m时,总有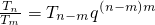 (q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件.
(q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件.
分析:(1)设m=1,则有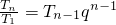 ,从而可得
,从而可得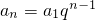 ,即可证得数列{an}是等比数列;
,即可证得数列{an}是等比数列;
(2)当q=1时,Tn•Tk=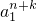 =
=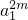 =
=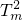 ;当q≠1时,
;当q≠1时,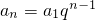 ,
,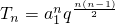 ,从而可得Tn•Tk=
,从而可得Tn•Tk=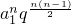 •
•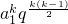 =
=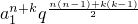 ,根据
,根据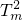 =
=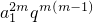 ,n+k=2m,k<m<n,利用基本不等式,即可得到结论;
,n+k=2m,k<m<n,利用基本不等式,即可得到结论;
(3)证明:由(1)知,充分性成立;
必要性:利用q≠1时,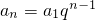 ,
,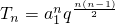 ,可证得
,可证得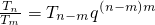 ,同理可证,当q=1时,也成立,故得证.
,同理可证,当q=1时,也成立,故得证.
点评:本题考查等比数列的定义,考查新定义,考查充要性的证明,综合性强,难度大.
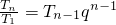 ,∴
,∴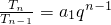
∴
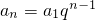
∴n≥2时,
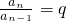
∴数列{an}是等比数列;
(2)解:当q=1时,an=a1,∴
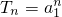 ,∴Tn•Tk=
,∴Tn•Tk=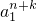 =
=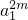 =
=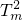
当q≠1时,
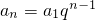 ,
,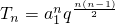
∴Tn•Tk=
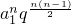 •
•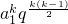 =
=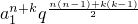
∵
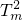 =
=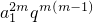 ,n+k=2m,k<m<n
,n+k=2m,k<m<n∴
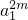 =
=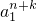 ,
,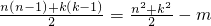 >
>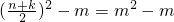
∴q>1时,Tn•Tk>
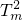 ;q<1时,Tn•Tk<
;q<1时,Tn•Tk<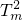
(3)证明:由(1)知,充分性成立;
必要性:若数列{an}是公比为q(q>0)的等比数列,则
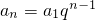
∴q≠1时,
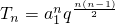
∴
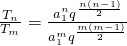 =
=
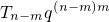 =
=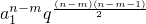 •q(n-m)m=
•q(n-m)m=
∴
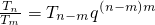
∴对?n,m∈N+,当n>m时,总有
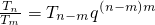 (q>0是常数)
(q>0是常数)同理可证,当q=1时,也成立
∴命题p:“对?n,m∈N+,当n>m时,总有
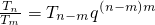 (q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件.
(q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件.分析:(1)设m=1,则有
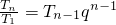 ,从而可得
,从而可得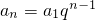 ,即可证得数列{an}是等比数列;
,即可证得数列{an}是等比数列;(2)当q=1时,Tn•Tk=
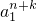 =
=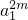 =
=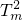 ;当q≠1时,
;当q≠1时,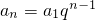 ,
,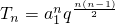 ,从而可得Tn•Tk=
,从而可得Tn•Tk=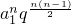 •
•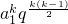 =
=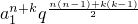 ,根据
,根据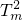 =
=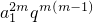 ,n+k=2m,k<m<n,利用基本不等式,即可得到结论;
,n+k=2m,k<m<n,利用基本不等式,即可得到结论;(3)证明:由(1)知,充分性成立;
必要性:利用q≠1时,
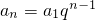 ,
,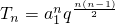 ,可证得
,可证得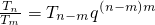 ,同理可证,当q=1时,也成立,故得证.
,同理可证,当q=1时,也成立,故得证.点评:本题考查等比数列的定义,考查新定义,考查充要性的证明,综合性强,难度大.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目