题目内容

已知sinA+sin3A+sin5A=a，cosA+cos3A+cos5A=b．求证：
（1）当b≠时，tg3A=
ab
．
（2）（1+2cos2A）2=a2+b2．
分析：（1）通过和差化积公式分别对sinA+sin3A+sin5A和cosA+cos3A+cos5A进行化简，最后两式相除即可证明．
（2）通过和差化积公式分别对sinA+sin3A+sin5A和cosA+cos3A+cos5A进行化简，两式分别平方后相加化简后即可证明结论．
解答：证明：（1）sinA+sin3A+sin5A=sinA+sin5A+sin3A
=2sin
A+5A
2
cos
5A-A
2
+sin3A
=2sin3A•cos2A+sin3A=sin3A（1+2cos2A），
∴sin3A（1+2cos2A）=a ①
同理有cos3A（1+2cos2A）=b ②
两式相除，即得tan3A=
a
b

（2）∵根据（1）sin3A（1+2cos2A）=a，①
cos3A（1+2cos2A）=b，②
∴①2+②2
sin23A（1+2cos2A）2+cos23A（1+2cos2A）2=a2+b2，
∴（1+2cos2A）2（sin23A+cos23A）=a2+b2，
∴（1+2cos2A）2=a2+b2．
点评：本题主要考查了三角函数恒等式的证明．证明此类题常涉及两角和公式、倍角公式、同角三角函数的关系等．公式多、难度大故应在这方面多下功夫．
练习册系列答案
相关题目
在△ABC中，已知tan
C
2
=sin（A+B），给出以下四个论断：
①tanA×cotB=1②1＜sinA+sinB≤
2

③sin2A+cos2B=1    ④sin2A+sin2B+sin2C=2
其中一定正确的是
 
（填上所有正确论断的序号）．
在△ABC中，内角A，B，C的对边分别为a，b，c，已知sinA=sin（A-B）+sinC．
（1）求角B的大小；
（2）若b2=ac，判断△ABC的形状；
（3）求证：
b•sin(C-
π
6
)
(2c-a)•cosB
为定值．

 [番茄花园1] （本题满分）在△ABC中，角A，B，C所对的边分别为a,b,c,设S为△ABC的面积，满足。

（Ⅰ）求角C的大小；

（Ⅱ）求的最大值。

 (Ⅰ)解：由题意可知

absinC=,2abcosC.

所以tanC=.

因为0<C<，

所以C=.

（Ⅱ)解：由已知sinA+sinB=sinA+sin(-C-A)=sinA+sin(-A)

                        =sinA+cosA+sinA=sin(A+)≤.

当△ABC为正三角形时取等号，

所以sinA+sinB的最大值是.

 

 

 [番茄花园1]1.

在△ABC中，内角A，B，C的对边分别为a，b，c，已知sinA=sin（A-B）+sinC．
（1）求角B的大小；
（2）若b2=ac，判断△ABC的形状；
（3）求证：
b•sin(C-
π
6
)
(2c-a)•cosB
为定值．

已知sina＝,aÎ(,p)，cosb＝－，b是第三象限的角.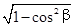

⑴ 求cos(a－b)的值；

⑵ 求sin(a＋b)的值；

⑶ 求tan2a的值.

【解析】第一问中∵ aÎ(,p),∴ cosa＝－＝－,  ∵ b是第三象限的角，

∴ sinb＝－＝－,     

cos(a－b)＝cosa·cosb＋sina·sinb ＝(－)×(－)＋×(－)＝－ 

⑵ 中sin(a＋b)＝sina·cosb＋cosa·sinb       ＝×(－)＋(－)×(－)＝ ⑶ 利用二倍角的正切公式得到。∵tana＝＝－ ∴tan2a＝ ＝＝－ 

解∵ aÎ(,p),∴ cosa＝－＝－,         …………1分

∵ b是第三象限的角，∴ sinb＝－＝－,        ………2分

⑴ cos(a－b)＝cosa·cosb＋sina·sinb          …………3分

＝(－)×(－)＋×(－)＝－          ………………5分

⑵ sin(a＋b)＝sina·cosb＋cosa·sinb          ……………………6分

＝×(－)＋(－)×(－)＝           …………………8分

⑶ ∵tana＝＝－             …………………9分

∴tan2a＝             ………………10分

＝＝－

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网