题目内容
已知sina= ,aÎ(
,aÎ( ,p),cosb=-
,p),cosb=- ,b是第三象限的角.
,b是第三象限的角.
⑴ 求cos(a-b)的值;
⑵ 求sin(a+b)的值;
⑶ 求tan2a的值.
【解析】第一问中∵ aÎ( ,p),∴ cosa=-
,p),∴ cosa=- =-
=- , ∵ b是第三象限的角,
, ∵ b是第三象限的角,
∴ sinb=-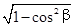 =-
=- ,
,
cos(a-b)=cosa·cosb+sina·sinb =(- )×(-
)×(- )+
)+ ×(-
×(- )=-
)=-
⑵ 中sin(a+b)=sina·cosb+cosa·sinb = ×(-
×(- )+(-
)+(- )×(-
)×(- )=
)= ⑶ 利用二倍角的正切公式得到。∵tana=
⑶ 利用二倍角的正切公式得到。∵tana= =-
=- ∴tan2a=
∴tan2a= =
= =-
=-
解∵ aÎ( ,p),∴ cosa=-
,p),∴ cosa=- =-
=- , …………1分
, …………1分
∵ b是第三象限的角,∴ sinb=-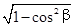 =-
=- , ………2分
, ………2分
⑴ cos(a-b)=cosa·cosb+sina·sinb …………3分
=(- )×(-
)×(- )+
)+ ×(-
×(- )=-
)=- ………………5分
………………5分
⑵ sin(a+b)=sina·cosb+cosa·sinb ……………………6分
= ×(-
×(- )+(-
)+(- )×(-
)×(- )=
)= …………………8分
…………………8分
⑶ ∵tana= =-
=- …………………9分
…………………9分
∴tan2a= ………………10分
………………10分
= =-
=-
【答案】
⑴ cos(a-b)=-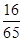 ⑵ sin(a+b)=
⑵ sin(a+b)= ⑶tan2a=-
⑶tan2a=-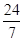

练习册系列答案
相关题目