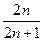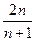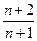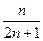题目内容
数列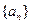 的各项均为正数,
的各项均为正数,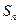 为其前
为其前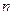 项和,对于任意
项和,对于任意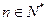 ,总有
,总有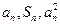 成等差数列.
成等差数列.
(1)求数列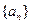 的通项公式;
的通项公式;
(2)设数列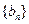 的前
的前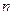 项和为
项和为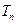 ,且
,且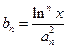 ,求证:对任意实数
,求证:对任意实数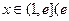 是常数,
是常数,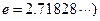 和任意正整数
和任意正整数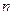 ,总有
,总有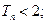
(3)正数数列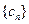 中,
中,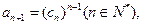 求数列
求数列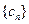 中的最大项.
中的最大项.
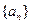 的各项均为正数,
的各项均为正数,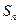 为其前
为其前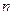 项和,对于任意
项和,对于任意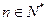 ,总有
,总有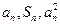 成等差数列.
成等差数列.(1)求数列
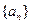 的通项公式;
的通项公式; (2)设数列
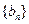 的前
的前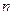 项和为
项和为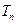 ,且
,且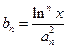 ,求证:对任意实数
,求证:对任意实数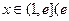 是常数,
是常数,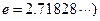 和任意正整数
和任意正整数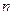 ,总有
,总有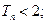
(3)正数数列
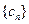 中,
中,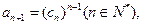 求数列
求数列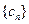 中的最大项.
中的最大项.(1)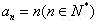 (2)略(3)
(2)略(3)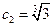
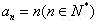 (2)略(3)
(2)略(3)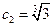
(1)由已知,对于任意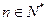 ,总有
,总有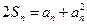 ①成立
①成立
所以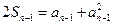 ②…………(1分)
②…………(1分)
①-②得,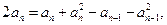
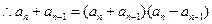
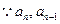 均为正数,
均为正数,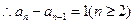
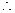 数列
数列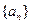 是公差为1的等差数列…………(3分)
是公差为1的等差数列…………(3分)
又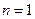 时,
时,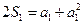 ,解得
,解得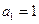
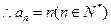 …………(5分)
…………(5分)
(2)证明: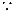 对任意实数
对任意实数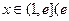 是常数,
是常数,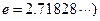 和任意正整数
和任意正整数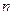 ,总有
,总有
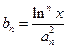
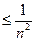 ,…………(6分)
,…………(6分)
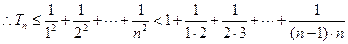
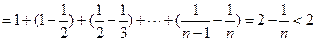 …………(9分)
…………(9分)
(3)由已知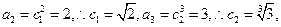
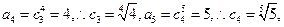
易得
猜想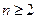 时,
时,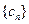 是递减数列…………(10分)
是递减数列…………(10分)
令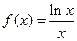
则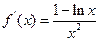 ,
,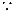 当
当 时,
时,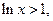 则
则 ,
,
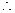 在
在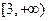 内,
内,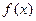 为单调递减函数,…………(12分)
为单调递减函数,…………(12分)
由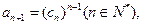 知
知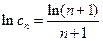
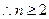 时,
时,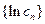 是递减数列,即
是递减数列,即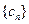 是递减数列,…………(13分)
是递减数列,…………(13分)
又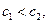
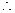 数列
数列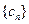 中的最大项为
中的最大项为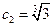 .…………(14分)
.…………(14分)
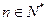 ,总有
,总有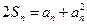 ①成立
①成立所以
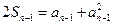 ②…………(1分)
②…………(1分)①-②得,
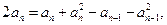
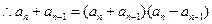
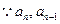 均为正数,
均为正数,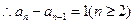
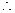 数列
数列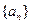 是公差为1的等差数列…………(3分)
是公差为1的等差数列…………(3分)又
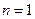 时,
时,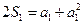 ,解得
,解得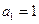
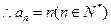 …………(5分)
…………(5分)(2)证明:
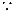 对任意实数
对任意实数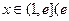 是常数,
是常数,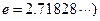 和任意正整数
和任意正整数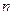 ,总有
,总有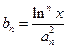
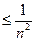 ,…………(6分)
,…………(6分)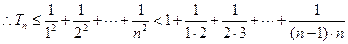
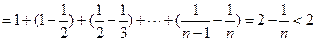 …………(9分)
…………(9分)(3)由已知
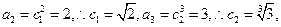
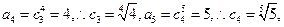
易得

猜想
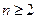 时,
时,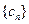 是递减数列…………(10分)
是递减数列…………(10分)令
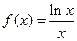
则
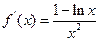 ,
,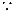 当
当 时,
时,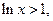 则
则 ,
,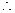 在
在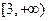 内,
内,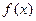 为单调递减函数,…………(12分)
为单调递减函数,…………(12分)由
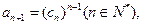 知
知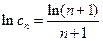
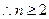 时,
时,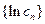 是递减数列,即
是递减数列,即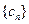 是递减数列,…………(13分)
是递减数列,…………(13分)又
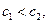
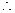 数列
数列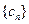 中的最大项为
中的最大项为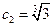 .…………(14分)
.…………(14分)
练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
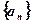 的前
的前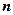 项和
项和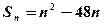 ,
,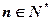 .
.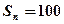 ,求
,求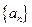 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表: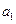
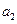
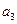


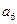



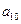
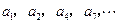 构成的数列为
构成的数列为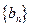 ,
,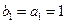 .
.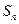 为数列
为数列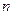 项和,且满足
项和,且满足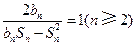 .
.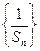 成等差数列,并求数列
成等差数列,并求数列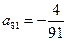 时,求上表中第
时,求上表中第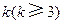 行所有项的和.
行所有项的和.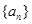 的前n项和
的前n项和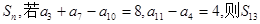 等于( )
等于( )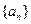 的前n项和为
的前n项和为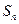 ,
,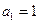 ,
,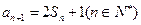 ,等差数列
,等差数列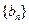 中
中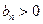
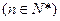 ,且
,且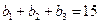 ,又
,又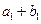 、
、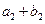 、
、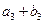 成等比数列.
成等比数列.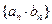 的前n项和
的前n项和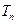 .
. 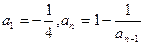
 ,求
,求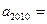
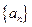 满足:
满足: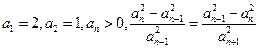
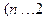 ,
,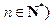 ,则
,则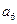 等于
等于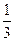
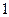
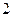
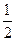
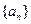 中,
中,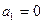 ,
, ,则
,则 ( )
( )



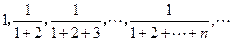 的前
的前 项和为( )
项和为( )