题目内容
设函数f(x)=ax2+lnx.(Ⅰ)当a=-1时,求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)已知a<0,若函数y=f(x)的图象总在直线
 的下方,求a的取值范围;
的下方,求a的取值范围;(Ⅲ)记f′(x)为函数f(x)的导函数.若a=1,试问:在区间[1,10]上是否存在k(k<100)个正数x1,x2,x3…xk,使得f′(x1)+f'(x2)+f′(x3)+…+f′(xk)≥2012成立?请证明你的结论.
【答案】分析:(Ⅰ)当a=-1时, ,f′(1)=-1,由此能求出函数y=f(x)的图象在点(1,f(1))处的切线方程.
,f′(1)=-1,由此能求出函数y=f(x)的图象在点(1,f(1))处的切线方程.
(Ⅱ) ,x>0,a<0.令f′(x)=0,则
,x>0,a<0.令f′(x)=0,则 .由此能求出a的取值范围.
.由此能求出a的取值范围.
(Ⅲ)当a=1时, .记g(x)=f′(x),其中x∈[1,10].由此入手能够推导出在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1,x2,x3…xk.
.记g(x)=f′(x),其中x∈[1,10].由此入手能够推导出在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1,x2,x3…xk.
解答:解:(Ⅰ)当a=-1时,f(x)=-x2+lnx, ,f′(1)=-1,
,f′(1)=-1,
所以切线的斜率为-1.…(2分)
又f(1)=-1,所以切点为(1,-1).
故所求的切线方程为:y+1=-(x-1)即x+y=0.…(4分)
(Ⅱ) ,x>0,a<0.…(6分)
,x>0,a<0.…(6分)
令f′(x)=0,则 .
.
当 时,f′(x)>0;当
时,f′(x)>0;当 时,f′(x)<0.
时,f′(x)<0.
故 为函数f(x)的唯一极大值点,
为函数f(x)的唯一极大值点,
所以f(x)的最大值为 =
= .…(8分)
.…(8分)
由题意有 ,解得
,解得 .
.
所以a的取值范围为 .…(10分)
.…(10分)
(Ⅲ)当a=1时, .记g(x)=f′(x),其中x∈[1,10].
.记g(x)=f′(x),其中x∈[1,10].
∵当x∈[1,10]时, ,∴y=g(x)在[1,10]上为增函数,
,∴y=g(x)在[1,10]上为增函数,
即y=f′(x)在[1,10]上为增函数.…(12分)
又 ,
,
所以,对任意的x∈[1,10],总有 .
.
所以f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≤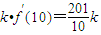 ,
,
又因为k<100,所以 .
.
故在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1,x2,x3…xk.…(14分)
点评:本题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想及有限与无限思想.
 ,f′(1)=-1,由此能求出函数y=f(x)的图象在点(1,f(1))处的切线方程.
,f′(1)=-1,由此能求出函数y=f(x)的图象在点(1,f(1))处的切线方程.(Ⅱ)
 ,x>0,a<0.令f′(x)=0,则
,x>0,a<0.令f′(x)=0,则 .由此能求出a的取值范围.
.由此能求出a的取值范围.(Ⅲ)当a=1时,
 .记g(x)=f′(x),其中x∈[1,10].由此入手能够推导出在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1,x2,x3…xk.
.记g(x)=f′(x),其中x∈[1,10].由此入手能够推导出在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1,x2,x3…xk.解答:解:(Ⅰ)当a=-1时,f(x)=-x2+lnx,
 ,f′(1)=-1,
,f′(1)=-1,所以切线的斜率为-1.…(2分)
又f(1)=-1,所以切点为(1,-1).
故所求的切线方程为:y+1=-(x-1)即x+y=0.…(4分)
(Ⅱ)
 ,x>0,a<0.…(6分)
,x>0,a<0.…(6分)令f′(x)=0,则
 .
.当
 时,f′(x)>0;当
时,f′(x)>0;当 时,f′(x)<0.
时,f′(x)<0.故
 为函数f(x)的唯一极大值点,
为函数f(x)的唯一极大值点,所以f(x)的最大值为
 =
= .…(8分)
.…(8分)由题意有
 ,解得
,解得 .
.所以a的取值范围为
 .…(10分)
.…(10分)(Ⅲ)当a=1时,
 .记g(x)=f′(x),其中x∈[1,10].
.记g(x)=f′(x),其中x∈[1,10].∵当x∈[1,10]时,
 ,∴y=g(x)在[1,10]上为增函数,
,∴y=g(x)在[1,10]上为增函数,即y=f′(x)在[1,10]上为增函数.…(12分)
又
 ,
,所以,对任意的x∈[1,10],总有
 .
.所以f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≤
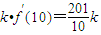 ,
,又因为k<100,所以
 .
.故在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1,x2,x3…xk.…(14分)
点评:本题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想及有限与无限思想.

练习册系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |