题目内容
17.已知定义在(0,+∞)上的函数f(x)同时满足下列三个条件:①f(2)=-1;②对任意实数x,y∈(0,+∞)都有f(xy)=f(x)+f(y);③当0<x<1时,f(x)>0.
(1)求f(4),f($\sqrt{2}$)的值;
(2)证明:函数f(x)在(0,+∞)上为减函数;
(3)解关于x的不等式f(2x)<f(x-1)-2.
分析 (1)根据条件②可分别令x=y=2和x=y=$\sqrt{2}$,便可得出f(4)=-2,$f(\sqrt{2})=-\frac{1}{2}$;
(2)根据单调性的定义,设任意的x1,x2∈(0,+∞),且x1<x2,作差f(x1)-f(x2),而条件中f(x)+f(y)可以变成f(xy),可考虑将这里的“-”号变成“+”号:可令x=x1,y=$\frac{1}{{x}_{1}}$,从而可以得到f(1)=$f({x}_{1})+f(\frac{1}{{x}_{1}})$,而可以求出f(1)=0,从而可得到$-f(x)=f(\frac{1}{x})$,这样便可得到$f({x}_{1})-f({x}_{2})=f({x}_{1})+f(\frac{1}{{x}_{2}})=f(\frac{{x}_{1}}{{x}_{2}})$,而由条件③可以得出f(x1)>f(x2),从而根据减函数的定义得到函数f(x)在(0,+∞)上为减函数;
(3)根据条件及求出的f(4)=-2,可将原不等式变成f(2x)<f(4x-4),这样根据f(x)的单调性便可得到$\left\{\begin{array}{l}{4x-4>0}\\{2x>4x-4}\end{array}\right.$,解该不等式便可得出原不等式的解.
解答 解:(1)令x=y=2得,f(2•2)=f(2)+f(2)=-2,∴f(4)=-2,令x=y=$\sqrt{2}$得,f($\sqrt{2}•\sqrt{2}$)=f($\sqrt{2}$)+f($\sqrt{2}$)=-1,∴$f(\sqrt{2})=-\frac{1}{2}$;
(2)设0<x1<x2;
先令x=x1,$y=\frac{1}{{x}_{1}}$,则$f({x}_{1}•\frac{1}{{x}_{1}})=f({x}_{1})+f(\frac{1}{{x}_{1}})$;
即$f(1)=f(x)+f(\frac{1}{x})$;
令x=x1,y=1,则f(x1•1)=f(x1)+f(1);
∴f(1)=0;
∴$f(x)+f(\frac{1}{x})=0$;
∴$-f(x)=f(\frac{1}{x})$;
∴$f({x}_{1})-f({x}_{2})=f({x}_{1})+f(\frac{1}{{x}_{2}})=f({x}_{1}•\frac{1}{{x}_{2}})$;
即$f({x}_{1})-f({x}_{2})=f(\frac{{x}_{1}}{{x}_{2}})$;
∵0<x1<x2;
∴$0<\frac{{x}_{1}}{{x}_{2}}<1$;
∵0<x<1时,f(x)>0;
∴$f(\frac{{x}_{1}}{{x}_{2}})>0$;
∴f(x1)>f(x2);
∴f(x)在(0,+∞)上为减函数;
(3)f(4)=-2;
∴由f(2x)<f(x-1)-2得,f(2x)<f(x-1)+f(4)=f(4(x-1));
∵f(x)在(0,+∞)上为减函数;
∴$\left\{\begin{array}{l}{x-1>0}\\{2x>4x-4}\end{array}\right.$;
∴1<x<2;
∴不等式的解为(1,2).
点评 考查对题中条件②的灵活运用,减函数的定义,以及根据减函数的定义证明一个函数为减函数的方法和过程,作差的方法比较f(x1)与f(x2),以及根据减函数的定义解不等式.

| A. | R | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0)∩(0,+∞) | D. | (-∞,0),(0,+∞) |
| A. | 有相同起点的向量 | B. | 平行向量 | ||
| C. | 模相等的向量 | D. | 相等向量 |
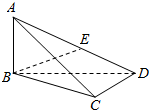 四面体ABCD中,AB⊥BC,AB⊥BD,BC⊥CD,且AB=BC=6,BD=8,E是AD中点,求BE与CD所成角的余弦值.
四面体ABCD中,AB⊥BC,AB⊥BD,BC⊥CD,且AB=BC=6,BD=8,E是AD中点,求BE与CD所成角的余弦值.