题目内容
5.设O为等边三角形ABC的中心,则向量$\overrightarrow{AO}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$是( )| A. | 有相同起点的向量 | B. | 平行向量 | ||
| C. | 模相等的向量 | D. | 相等向量 |
分析 根据平面向量的基本概念与等边三角形的性质,即可得出答案.
解答 解:如图所示,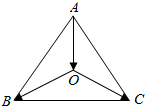
O是等边△ABC的中心,
∴向量$\overrightarrow{AO}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$的模长相等.
故选:C.
点评 本题考查了平面向量的应用问题,是基础题目.

练习册系列答案
相关题目
13.如图,向量$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AC}=\overrightarrow{b}$,$\overrightarrow{CD}=\overrightarrow{c}$,则向量$\overrightarrow{BD}$可以表示为( )


| A. | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | B. | $\overrightarrow{b}$+$\overrightarrow{a}$-$\overrightarrow{c}$ | C. | $\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\overrightarrow{b}$-$\overrightarrow{a}$+$\overrightarrow{c}$ |
10.下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( )
| A. | y=x3 | B. | y=|x+1| | C. | y=-x2+1 | D. | y=2|x|+1 |
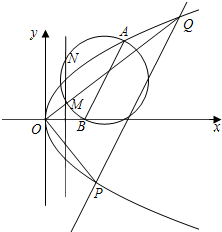 已知A是抛物线y2=4x上的一点,以点A和点B(2,0)为直径的圆C交直线x=1于M,N两点.直线l与AB平行,且直线l交抛物线于P,Q两点.
已知A是抛物线y2=4x上的一点,以点A和点B(2,0)为直径的圆C交直线x=1于M,N两点.直线l与AB平行,且直线l交抛物线于P,Q两点.