题目内容
【题目】如图,四棱锥![]() 中,
中,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点.
中点.
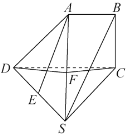
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 为线段
为线段![]() 的中点,求二面角
的中点,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,证出
,证出![]() ,利用线面平行的判定定理即可证出.
,利用线面平行的判定定理即可证出.
(2)不妨设![]() ,则
,则![]() ,
,![]() ,取
,取![]() 中点
中点![]() ,得
,得![]() ,
,![]() ,以
,以![]() 为原点,以
为原点,以![]() 为
为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 的一个法向量与平面
的一个法向量与平面![]() 的一个法向量,利用空间向量的数量积即可求解.
的一个法向量,利用空间向量的数量积即可求解.
证明:(1)如图,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
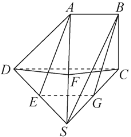
因为![]() 为
为![]() 中位线,
中位线,
所以![]() 且
且![]() ,
,
又因为![]() 且
且![]() ,
,
所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)不妨设![]() ,则
,则![]() ,
,![]() ,取
,取![]() 中点
中点![]() ,
,
所以![]() ,
,
又因为![]() ,
,![]() ,
,
所以四边形![]() 为矩形,
为矩形,
所以![]() ,
,![]() ,
,
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() ,
,
又因为三角形![]() 为正三角形,
为正三角形,
所以![]() ,
,
故如图建立空间直角坐标系![]() ,
,
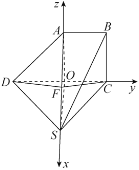
可得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,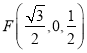 ,
,
所以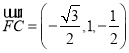 ,
,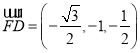 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则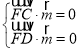 ,可取
,可取![]() ,
,
易知平面![]() 的一个法向量
的一个法向量![]() ,
,
所以![]() ,又知二面角
,又知二面角![]() 为锐角,
为锐角,
则二面角![]() 的大小为
的大小为![]() .
.

【题目】以昆明、玉溪为中心的滇中地区,冬无严寒、夏无酷暑,世界上主要的鲜切花品种在这里都能实现周年规模化生产.某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰,由于库房限制每天最多加工6箱.
(1)若某天该鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,则恰好一位是以2000元价格购买的顾客,另一位是以1200元价格购买的顾客的概率是多少?
(2)该鲜花批发店统计了100天内该种玫瑰在每天下午3点以前的销售量![]() (单位:箱),统计结果如下表所示(视频率为概率):
(单位:箱),统计结果如下表所示(视频率为概率):
| 4 | 5 | 6 |
频数 | 30 |
|
|
①估计接下来的一个月(30天)内该种玫瑰每天下午3点以前的销售量不少于5箱的天数是多少?
②若批发店每天在购进5箱数量的玫瑰时所获得的平均利润最大(不考虑其他成本),求![]() 的取值范围.
的取值范围.
【题目】近几年来我国电子商务行业发展迅猛,2016年元旦期间,某购物平台的销售业绩高达918亿人民币,与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)完成商品和服务评价的![]() 列联表,并说明是否可以在犯错误的概率不超过
列联表,并说明是否可以在犯错误的概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品和服务全好评的次数为随机变量![]() .
.
①求对商品和服务全好评的次数![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②求![]() 的数学期望和方差.
的数学期望和方差.
参考数据及公式如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(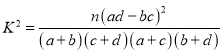 ,其中
,其中![]() )
)