题目内容
（08年平遥中学） 已知双曲线
的焦点为F1、F2，以F1F2为直径的圆与双曲线的一个交点为M，且tan∠M F1F2=
，则双曲线的离心率为
A．
B．
C．2 D．
答案：A
解析：
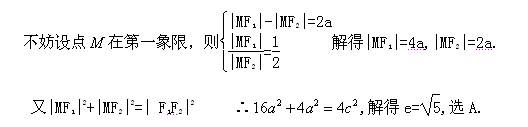
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
心算口算巧算一课一练系列答案题目内容
（08年平遥中学） 已知双曲线的焦点为F1、F2，以F1F2为直径的圆与双曲线的一个交点为M，且tan∠M F1F2=，则双曲线的离心率为
A． B． C．2 D．
答案：A
解析：
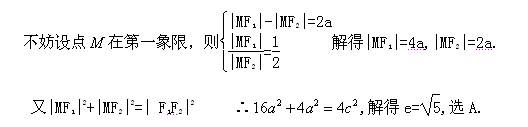
心算口算巧算一课一练系列答案
的大小关系是
或α≤
ln(1-x)(a∈R)，e为自然对数的底数。
)(1+
)…(1+
)与e的大小并给出证明（其中n≥2,n∈N*）。
的最小值为 ．