Question

【题目】设是同一球面上的四点，是边长为6的等边三角形，若三棱锥体积的最大值为，则该球的表面积为（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

作出图形由图知，当点D与球心O以及△ABC外接圆圆心三点共线且D与△ABC外接圆圆心位于球心的异侧时，三棱锥D﹣ABC的体积取得最大值，结合三棱锥的体积求出棱锥的h，然后利用勾股定理求球O的半径R，最后利用表面积公式可求出答案．

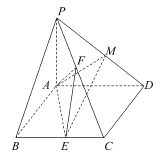
如图所示，

由题意可知，设点M为△ABC外接圆的圆心，当点D、O、M三点共线时，且D、M分别位于点O的异侧时，三棱锥D﹣ABC的体积取得最大值，

△ABC的面积为，

由于三棱锥D﹣ABC的体积的最大值为，得DM＝6，

易知DM⊥平面ABC，则三棱锥D﹣ABC为正三棱锥，△ABC的外接圆直径为2AM=，∴AM=2，设球O的半径为为R，在直角三角形AOM中，

由勾股定理得,即,解得R=4或R=6(舍去)

因此，球O的表面积为．

故选：A．