题目内容
( 分)
分)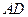 是直角三角形
是直角三角形 斜边
斜边 上的高,(
上的高,(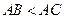 ),
),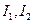 分别是
分别是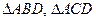 的内心,
的内心,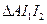 的外接圆
的外接圆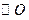 分别交
分别交 于
于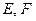 ,直线
,直线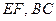 交于点
交于点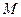 ;证明:
;证明: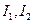 分别是
分别是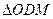 的内心与旁心.
的内心与旁心.
 分)
分)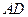 是直角三角形
是直角三角形 斜边
斜边 上的高,(
上的高,(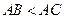 ),
),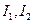 分别是
分别是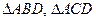 的内心,
的内心,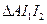 的外接圆
的外接圆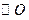 分别交
分别交 于
于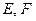 ,直线
,直线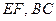 交于点
交于点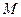 ;证明:
;证明: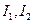 分别是
分别是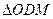 的内心与旁心.
的内心与旁心.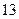
略
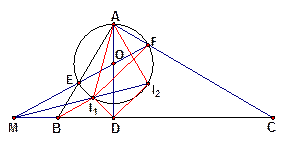
:如图,连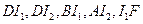 ,由
,由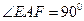 ,则圆心
,则圆心 在
在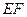 上,设直径
上,设直径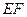 交
交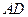 于
于 ,并简记
,并简记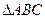 的三内角为
的三内角为 ,由
,由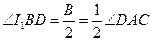
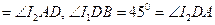 ,
,
所以 ∽
∽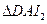 ,得
,得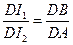 ,且
,且 ,故
,故 ∽
∽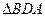 ,而
,而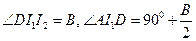 ,
,
注意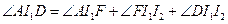 ,
,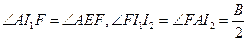 ,
,
所以 ,因此
,因此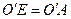 ,同理得
,同理得 ,故
,故 与
与 重合,即圆心
重合,即圆心 在
在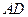 上,而
上,而 ,
,
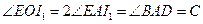 ,所以
,所以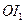 平分
平分 ;
;
同理得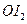 平分
平分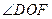 ,即
,即 是
是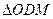 的内心,
的内心,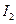 是
是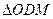 的旁心.
的旁心.
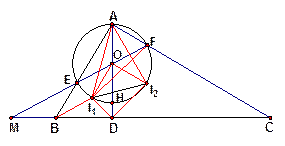
证二:如图,因为 ,故
,故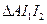 的外接圆圆心
的外接圆圆心 在
在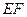 上,连
上,连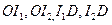 ,则由
,则由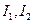 为内心知,
为内心知,
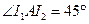 , 所以
, 所以
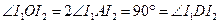 ,
,
于是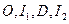 四点共圆,所以
四点共圆,所以
 ,又因
,又因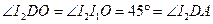 ,因此点
,因此点 在
在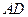 上,即
上,即 为
为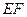 与
与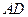 的交点.设
的交点.设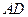 与
与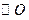 交于另一点
交于另一点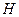 ,而由
,而由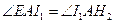 ,
,
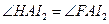 ,可知,
,可知,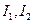 分别为
分别为 的中点,所以
的中点,所以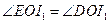 ,
,
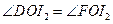 .因此,点
.因此,点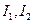 分别为
分别为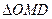 的内心与旁心.
的内心与旁心.
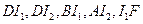 ,由
,由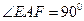 ,则圆心
,则圆心 在
在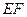 上,设直径
上,设直径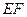 交
交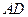 于
于 ,并简记
,并简记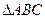 的三内角为
的三内角为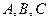 ,由
,由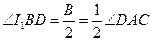


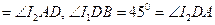 ,
,所以
 ∽
∽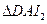 ,得
,得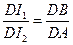 ,且
,且 ,故
,故 ∽
∽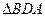 ,而
,而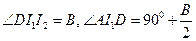 ,
,注意
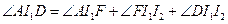 ,
,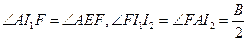 ,
,所以
 ,因此
,因此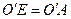 ,同理得
,同理得 ,故
,故 与
与 重合,即圆心
重合,即圆心 在
在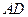 上,而
上,而 ,
,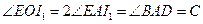 ,所以
,所以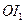 平分
平分 ;
;同理得
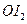 平分
平分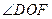 ,即
,即 是
是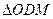 的内心,
的内心,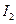 是
是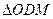 的旁心.
的旁心.证二:如图,因为
 ,故
,故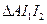 的外接圆圆心
的外接圆圆心 在
在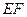 上,连
上,连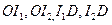 ,则由
,则由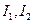 为内心知,
为内心知,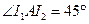 , 所以
, 所以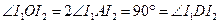 ,
,于是
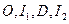 四点共圆,所以
四点共圆,所以 ,又因
,又因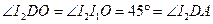 ,因此点
,因此点 在
在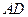 上,即
上,即 为
为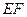 与
与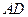 的交点.设
的交点.设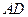 与
与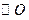 交于另一点
交于另一点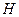 ,而由
,而由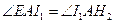 ,
,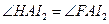 ,可知,
,可知,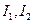 分别为
分别为 的中点,所以
的中点,所以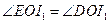 ,
,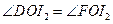 .因此,点
.因此,点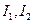 分别为
分别为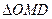 的内心与旁心.
的内心与旁心.
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 和B
和B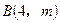 并且与
并且与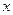 轴相切的圆有且只有一个,求实数
轴相切的圆有且只有一个,求实数 的值和这个圆的方程。
的值和这个圆的方程。
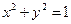 与直线
与直线 没有公共点的充要条件是( )
没有公共点的充要条件是( )

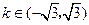
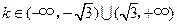
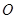 引圆
引圆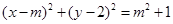 的切线
的切线 ,当
,当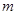 变化时,切点
变化时,切点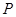 的轨迹方程是( )
的轨迹方程是( )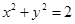

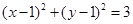
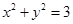
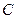 和
和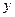 轴相切,圆心在直线
轴相切,圆心在直线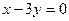 上,且被直线
上,且被直线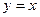 截得的弦长为
截得的弦长为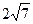
 ,求圆
,求圆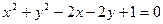 上的点到直线
上的点到直线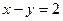 的距离最大值是( )
的距离最大值是( )