题目内容
已知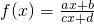
（a、b、c、d均不为零），试问：a、b、c、d满足什么条件时，它的反函数是它自身．
解：设：y=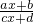
，
则：x=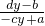
，
∴f（x）的反函数是：
y=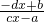
要使f（x）的反函数是它自身，
则有：a=-d，
∴a=-d时，它的反函数是它自身．
分析：从条件中函数式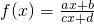（a、b、c、d均不为零）中反解出x，再将x，y互换得到的函数与原函数是同一个函数，最后比照系数即可．
点评：求反函数，一般应分以下步骤：（1）由已知解析式y=f（x）反求出x=Ф（y）；（2）交换x=Ф（y）中x、y的位置；（3）求出反函数的定义域（一般可通过求原函数的值域的方法求反函数的定义域）．
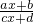，则：x=
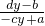，∴f（x）的反函数是：
y=
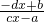
要使f（x）的反函数是它自身，
则有：a=-d，
∴a=-d时，它的反函数是它自身．
分析：从条件中函数式
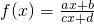（a、b、c、d均不为零）中反解出x，再将x，y互换得到的函数与原函数是同一个函数，最后比照系数即可．点评：求反函数，一般应分以下步骤：（1）由已知解析式y=f（x）反求出x=Ф（y）；（2）交换x=Ф（y）中x、y的位置；（3）求出反函数的定义域（一般可通过求原函数的值域的方法求反函数的定义域）．
练习册系列答案
相关题目