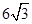题目内容
已知双曲线C1: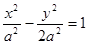 (a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(1)求证:C1,C2总有两个不同的交点;
(2)问:是否存在过C2的焦点F1的弦AB,使ΔAOB的面积有最大值或最小值?若存在,求直线AB的方程与SΔAOB的最值,若不存在,说明理由。
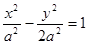 (a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。(1)求证:C1,C2总有两个不同的交点;
(2)问:是否存在过C2的焦点F1的弦AB,使ΔAOB的面积有最大值或最小值?若存在,求直线AB的方程与SΔAOB的最值,若不存在,说明理由。
(1)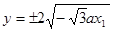 (因为x1≠0),所以C1,C2总有两个不同交点。
(因为x1≠0),所以C1,C2总有两个不同交点。
(2)存在过F的直线x=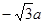 使ΔAOB面积有最小值6a2
使ΔAOB面积有最小值6a2
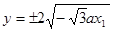 (因为x1≠0),所以C1,C2总有两个不同交点。
(因为x1≠0),所以C1,C2总有两个不同交点。(2)存在过F的直线x=
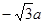 使ΔAOB面积有最小值6a2
使ΔAOB面积有最小值6a2(1)由双曲线方程得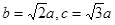 ,所以F1(
,所以F1(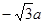 ,0),抛物线焦点到准线的距离
,0),抛物线焦点到准线的距离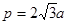 ,抛物线:
,抛物线: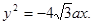 ①
①
把①代入C1方程得: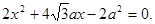 ②
②
Δ=64a2>0,所以方程②必有两个不同实根,设为x1,x2,由韦达定理得x1x2=-a2<0,所以②必有一个负根设为x1,把x1代入①得y2=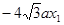 ,所以
,所以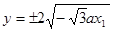 (因为x1≠0),所以C1,C2总有两个不同交点。
(因为x1≠0),所以C1,C2总有两个不同交点。
(2)设过F1(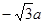 ,0)的直线AB为my=(x+
,0)的直线AB为my=(x+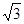 a),由
a),由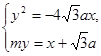 得y2+4
得y2+4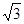 may-12a2=0,因为Δ=48m2a2+48a2>0,设y1,y2分别为A,B的纵坐标,则y1+y2=
may-12a2=0,因为Δ=48m2a2+48a2>0,设y1,y2分别为A,B的纵坐标,则y1+y2=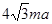 ,y1y2=-12a2.所以(y1-y2)2=48a2(m2+1).所以SΔAOB=
,y1y2=-12a2.所以(y1-y2)2=48a2(m2+1).所以SΔAOB=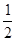 |y1-y2|•|OF1|=
|y1-y2|•|OF1|=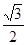 a•
a•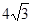 a•
a•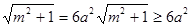 ,当且仅当m=0时,SΔAOB的面积取最小值;当m→+∞时,SΔAOB→+∞,无最大值。所以存在过F的直线x=
,当且仅当m=0时,SΔAOB的面积取最小值;当m→+∞时,SΔAOB→+∞,无最大值。所以存在过F的直线x=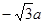 使ΔAOB面积有最小值6a2。
使ΔAOB面积有最小值6a2。
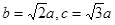 ,所以F1(
,所以F1(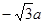 ,0),抛物线焦点到准线的距离
,0),抛物线焦点到准线的距离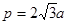 ,抛物线:
,抛物线: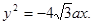 ①
①把①代入C1方程得:
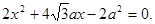 ②
②Δ=64a2>0,所以方程②必有两个不同实根,设为x1,x2,由韦达定理得x1x2=-a2<0,所以②必有一个负根设为x1,把x1代入①得y2=
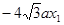 ,所以
,所以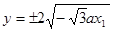 (因为x1≠0),所以C1,C2总有两个不同交点。
(因为x1≠0),所以C1,C2总有两个不同交点。(2)设过F1(
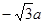 ,0)的直线AB为my=(x+
,0)的直线AB为my=(x+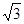 a),由
a),由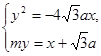 得y2+4
得y2+4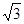 may-12a2=0,因为Δ=48m2a2+48a2>0,设y1,y2分别为A,B的纵坐标,则y1+y2=
may-12a2=0,因为Δ=48m2a2+48a2>0,设y1,y2分别为A,B的纵坐标,则y1+y2=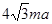 ,y1y2=-12a2.所以(y1-y2)2=48a2(m2+1).所以SΔAOB=
,y1y2=-12a2.所以(y1-y2)2=48a2(m2+1).所以SΔAOB=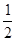 |y1-y2|•|OF1|=
|y1-y2|•|OF1|=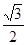 a•
a•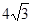 a•
a•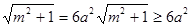 ,当且仅当m=0时,SΔAOB的面积取最小值;当m→+∞时,SΔAOB→+∞,无最大值。所以存在过F的直线x=
,当且仅当m=0时,SΔAOB的面积取最小值;当m→+∞时,SΔAOB→+∞,无最大值。所以存在过F的直线x=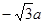 使ΔAOB面积有最小值6a2。
使ΔAOB面积有最小值6a2。
练习册系列答案
相关题目
 轴上动点
轴上动点 引抛物线
引抛物线 的两条切线
的两条切线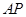 、
、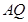 ,
,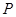 、
、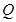 为切点.
为切点.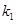 和
和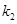 ,求证:
,求证: 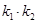 为定值,并求出定值;
为定值,并求出定值;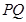 恒过定点,并求出定点坐标;
恒过定点,并求出定点坐标; 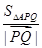 最小时,求
最小时,求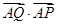 的值.
的值.
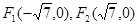 离心率e=
离心率e=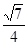 (1)求椭圆的方程。(2)若CD为过左焦点
(1)求椭圆的方程。(2)若CD为过左焦点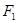 的弦,求
的弦,求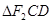 的周长
的周长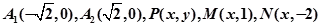 ,若实数
,若实数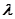 使得
使得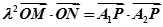 (
(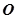 为坐标原点)
为坐标原点)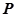 点的轨迹方程,并讨论
点的轨迹方程,并讨论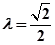 时,若过点
时,若过点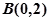 的直线与(1)中
的直线与(1)中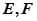 (
(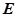 在
在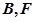 之间),试求
之间),试求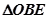 与
与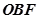 面积之比的取值范围。
面积之比的取值范围。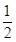 ,点P(1,
,点P(1,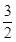 )和A、B都在椭圆E上,且
)和A、B都在椭圆E上,且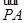 +
+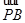 =m
=m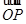 (m∈R).
(m∈R).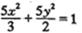
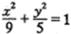
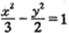

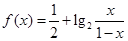 的图象上任两点,且
的图象上任两点,且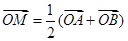 ,已知点M横坐标为
,已知点M横坐标为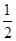 ,
,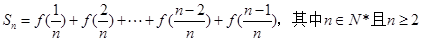 ,求Sn。
,求Sn。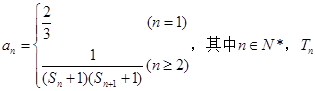 为数列{an}的前n项和, 若
为数列{an}的前n项和, 若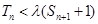 对一切
对一切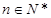 都成立,求
都成立,求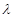 取值范围。
取值范围。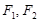 分别是双曲线
分别是双曲线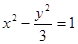 的左、右焦点,
的左、右焦点,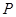 是双曲线上一点,且满足
是双曲线上一点,且满足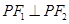 ,则
,则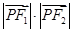 的值是( )
的值是( )