题目内容
函数f(x)的定义域为D,如果存在x0∈D,使f(x0)=x0,则称点(x0,x0)为函数f(x)图象上的不动点.
(1)试证明:若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个.
(2)若函数f(x)= 的图象上有两个关于直线x+y=3对称的不动点,求a的值.
的图象上有两个关于直线x+y=3对称的不动点,求a的值.
答案:
解析:
解析:
|
解(1)因为f(x)是奇函数,所以f(-x)=-f(x).又因为x∈R,令x=0,所以f(0)=0. 所以(0,0)是奇函数f(x)的一个不动点.设c≠0,(c,c)是f(x)的一个不动点,f(c)=c.由于f(-c)=-f(c)=-c,所以(-c,-c)也是f(x)的一个不动点.且-c≠c,即奇函数f(x)的非零不动点如果存在,则必成对.又因为f(x)只有有限个不动点,所以不动点数目是奇数个. (2)设点(x0,x0)是f(x)= 整理得,x2+(a-2)x-4=0,由韦达定理得,-(a-2)=x0+(3-x0),a=-1故f(x)= |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
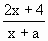 图象上的一个不动点,则(x0,x0)关于直线x+y=3的对称点(3-x0,3-x0)也是f(x)的不动点,即x0,3-x0是方程x=
图象上的一个不动点,则(x0,x0)关于直线x+y=3的对称点(3-x0,3-x0)也是f(x)的不动点,即x0,3-x0是方程x=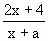 的两个根.
的两个根.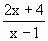 .
.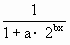 的定义域为R,且
的定义域为R,且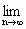 f(-n)=0(n∈N).
f(-n)=0(n∈N).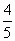 且f(0)=
且f(0)=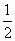 ,求证:f(1)+f(2)+…+f(n)>n+
,求证:f(1)+f(2)+…+f(n)>n+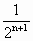 -
-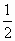 (n∈N).
(n∈N).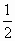 ,求证:f(1)+f(2)+…+f(n)>n+
,求证:f(1)+f(2)+…+f(n)>n+