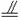题目内容
设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
90°
解析:
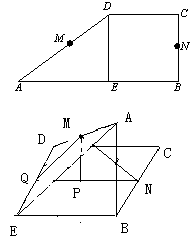
如左图,在平面AED内作MQ∥AE交ED于Q,则MQ⊥ED,且Q为ED的中点,连结QN,则NQ⊥ED且QN∥EB,QN=EB,∠MQN为二面角A-DE-B的平面角,∴∠MQN=45°,∵AB⊥平面BCDE,又∠AEB=∠MQN=45°,MQ=![]() AE=
AE=![]() EB,在平面MQN内作MP⊥BQ,得QP=MP=
EB,在平面MQN内作MP⊥BQ,得QP=MP=![]() EB,故PB=QP=
EB,故PB=QP=![]() EB,故QMN是以∠QMN为直角的等腰三角形,即MN⊥QM,也即MN子AE所成角大小等于90°
EB,故QMN是以∠QMN为直角的等腰三角形,即MN⊥QM,也即MN子AE所成角大小等于90°

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
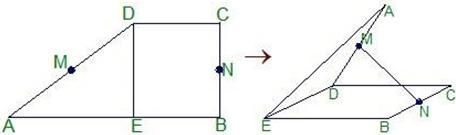
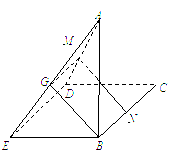 设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E (如图). 现将
设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E (如图). 现将