题目内容
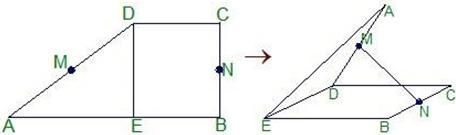
12、设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E（如图）、现将△ADE沿DE折起，使二面角A-DE-B为45°，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小等于
90°
．分析：先取AB的中点P，将MN平移到PB，则锐角∠APB就是异面直线MN与AE所成的角，在三角形ABE中再利用等腰直角三角形的中线就是高这一原理即可求出所成角．
解答：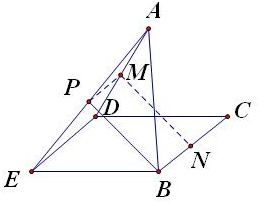
解：如图，取AE的中点P，连接PB，PM，
∵PM∥ED，ED∥BC，∴PM∥BN，且PM=BN，
∴四边形PMNB为平行四边形则MN∥PB
∵AB⊥EB，∠AEB=45°∴BP⊥AE，而MN∥PB
∴AE⊥MN，M、N的连线与AE所成角的大小等于90°，
故答案为90°．
解：如图，取AE的中点P，连接PB，PM，∵PM∥ED，ED∥BC，∴PM∥BN，且PM=BN，
∴四边形PMNB为平行四边形则MN∥PB
∵AB⊥EB，∠AEB=45°∴BP⊥AE，而MN∥PB
∴AE⊥MN，M、N的连线与AE所成角的大小等于90°，
故答案为90°．
点评：本小题主要考查异面直线所成的角，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
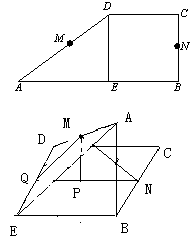
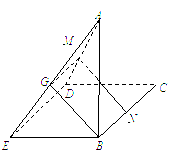设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E (如图). 现将
沿DE折起，使二面角
的大小为
，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小为 .
