Question

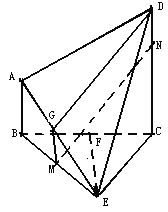
【题目】如图，直角梯形中， , ,平面平面, 为等边三角形， 分别是的中点， .

(1)证明： ;

(2)证明： 平面;

(3)若,求几何体的体积.

Answer 1

【答案】（1）由为等边三角形， 是的中点知，由平面平面及面面垂直性质定理知， 平面，再由线面垂直定义得EF⊥CD；（2）取AE的中点G，连结MG，DG，因为M是BE的中点，所以MG∥且等于AB的一半，又因为AB∥CD且AB= ， ，所以DN平行且等于MG，所以MGDN是平行四边形，所以MN∥DG，由线面平行的判定定理可得MN∥面ADE；（3）由（1）知EF⊥面ABCD，所以EF是四棱锥E-ABCD的高，由△BEC为正三角形，BC=2，可求得EF的长，由题知ABCD为直角梯形，AB⊥BC，AB=1，BC=2，所以DC=2AB=2，可求出底面ABCD的面积，所以四棱锥D-ABCD的体积就等于.

【解析】试题分析：（1）（2）（3）

试题解析：(1)证明： 为等边三角形， 是的中点

1分

又因为平面平面，交线为, 平面

根据面面垂直的性质定理得平面; 3分

又 平面

4分

(2)证明：取中点G，连接

,且6分

,

,且8分

四边形是平行四边形

9分

又 平面， 平面

平面10分

(3)解：依题，直角梯形中，

则直角梯形的面积为12分

由（1）可知平面， 是四棱锥的高

在等边中，由边长,得13分

故几何体的体积为

14分

考点: 线面垂直定义；面面垂直性质定理；线面平行的判定；简单几何体体积计算；逻辑推理能力；运算求解能力