题目内容
【题目】已知抛物线C:x2=8y.AB是抛物线C的动弦,且AB过F(0,2),分别以A,B为切点作轨迹C的切线,设两切线交点为Q,证明:AQ⊥BQ.
【答案】证明:∵直线AB与x轴不垂直,设AB:y=kx+2,A(x1 , y1),B(x2 , y2).
由 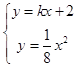 得到x2﹣8kx﹣16=0,x1+x2=8k,x1x2=﹣16,
得到x2﹣8kx﹣16=0,x1+x2=8k,x1x2=﹣16,
抛物线方程为y= ![]() x2 ,
x2 ,
∴y′= ![]() x
x
∴过抛物线上A、B两点的切线斜率分别是k1= ![]() x1 , k2=
x1 , k2= ![]() x2 ,
x2 ,
∴k1k2= ![]() x1
x1 ![]() x2=﹣1,
x2=﹣1,
∴AQ⊥BQ
【解析】设AB:y=kx+2,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系利用切线的几何意义即可求得过抛物线上A、B两点的切线斜率关系,从而解决问题

练习册系列答案
相关题目