题目内容
函数f(x)的定义域为D，满足：①f(x)在D内是单调函数；②存在[
]
D，使得f(x)在[]上的值域为[a，b]，那么就称函数y=f(x)为“优美函数”，若函数f(x)=logc(cx－t)(c＞0，c≠1)是“优美函数”，则t的取值范围为( )
| A．(0，1) | B．(0， ) | C．(－∞， ) | D．(0，) |
D
解析试题分析：由f(x)＝f(x)=logc(cx－t)（c＞0，c≠1）是“优美函数”，知f（x）在其定义域内为增函数，因为f(x)在[]上的值域为[a，b]，所以方程f（x）= f(x)=logc(cx－t)=x至少有两个根，故cx-t=
，由此能求出t的取值范围．
考点：函数性质的应用.
练习册系列答案
导学教程高中新课标系列答案
相关题目
若不等式
对任意的
恒成立，则
的取值范围是（ ）
A． | B． | C． | D． |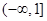
对任意实数a,b定义运算
如下
，则函数
的值域为 ( )
A． | B． | C． | D． |
，且函数
有且只有一个零点，则实数
的取值范围是( )
B．
.
D．
设x，y∈R，且4xy＋4y2＋x＋6＝0，则x的取值范围是 ( )
| A．－3≤x≤2 | B．－2≤x≤3 |
| C．x≤－2或x≥3 | D．x≤－3或x≥2 |
已知函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x).当0≤x≤1时,f(x)=x2.若直线y=x+a与函数y=f(x)的图象在[0,2]内恰有两个不同的公共点,则实数a的值是( )
| A．0 | B．0或- |
C．- 或- | D．0或- |
，P4(2,2)中，“好点”的个数为( )设a＝log36，b＝log510，c＝log714，则( )
| A．c＞b＞a | B．b＞c＞a |
| C．a＞c＞b | D．a＞b＞c |
函数f(x)=2x-cosx在[0,+∞)内( )
| A．没有零点 | B．有且仅有一个零点 |
| C．有且仅有两个零点 | D．有无穷多个零点 |