题目内容
已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除.当地有关部门决定每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房.
(1)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
(2)按照(1)的拆除速度,至少需多少年才能使该地的住房面积比今年年初的住房面积翻一番.(取lg 3=0.477,lg 1.1=0.041)
(1)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
(2)按照(1)的拆除速度,至少需多少年才能使该地的住房面积比今年年初的住房面积翻一番.(取lg 3=0.477,lg 1.1=0.041)
分析:(1)根据每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房,可得第五年末的住房面积,利用第五年末该地的住房面积正好比今年年初的住房面积增加了30%,建立方程,即可求得每年拆除的旧住房面积;
(2)确定第n年末的住房面积,根据住房面积比今年年初的住房面积翻一番,建立不等式,即可求得结论.
(2)确定第n年末的住房面积,根据住房面积比今年年初的住房面积翻一番,建立不等式,即可求得结论.
解答:解:(1)第一年末的住房面积为1.1a-b(m2);第二年末的住房面积为(1.1a-b)×1.1-b=1.21a-2.1b(m2)
第五年末的住房面积为a•(
)5-b•[1+
+(
)2+(
)3+(
)4]=1.6a-6ba------(4分)
依题意可知1.6a-6b=1.3a,解得b=
,
所以每年拆除的旧住房面积为
(m2)-------------------------------------(6分)
(2)由(1)知第n年末的住房面积为1.1na-
b=1.1na-
×
所以1.1na-
×
≥2a-------------------------------------(8分)
即1.1n≥3所以n≥log1.13≈11.5-------------------------------------(10分)
所以至少需12年才能使该地的住房面积比今年年初的住房面积翻一番.------------(12分)
第五年末的住房面积为a•(
| 11 |
| 10 |
| 11 |
| 10 |
| 11 |
| 10 |
| 11 |
| 10 |
| 11 |
| 10 |
依题意可知1.6a-6b=1.3a,解得b=
| a |
| 20 |
所以每年拆除的旧住房面积为
| a |
| 20 |
(2)由(1)知第n年末的住房面积为1.1na-
| 1-1.1n |
| 1-1.1 |
| 1.1n-1 |
| 0.1 |
| a |
| 20 |
所以1.1na-
| 1.1n-1 |
| 0.1 |
| a |
| 20 |
即1.1n≥3所以n≥log1.13≈11.5-------------------------------------(10分)
所以至少需12年才能使该地的住房面积比今年年初的住房面积翻一番.------------(12分)
点评:本题考查数列模型的构建,考查解不等式,解题的关键是正确建立数列模型,属于中档题.

练习册系列答案
相关题目
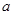 (单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房。
(单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房。